Barras retas de 6 mm de diâmetro e 30 cm de comprimento são enroladas e armazenadas dentro de um tambor de 1,25m de diâmetro interno. Considerando que a resistência ao escoamento não deve ser excedida, determinar:

1. A máxima tensão em uma barra enrolada;
2. O correspondente momento fletor em uma barra. Usar .

No item a) queremos determinar a máxima tensão que age na nossa lâmina, sabemos que a nossa fórmula é dada por:

Dessa fórmula sabemos que:

Para determinarmos a máxima deformação, devemos usar a seguinte fórmula:

Sabemos que é o raio da nossa barra, e a espessura da nossa barra é dada por , sendo assim teremos que:

O já e o nosso velho conhecido raio de curvatura, e o raio de curvatura deve englobar tanto o raio do tambor quanto o raio da barra, mas aqui temos que pensar da seguinte maneira:

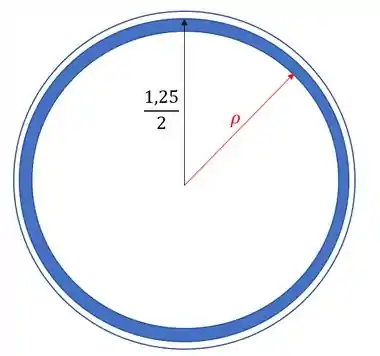
Perceba que quando colocamos a barra dentro do tambor, ela irá encurtar o raio de curvatura, porque ela vai estar ocupando a parte interna do tambor, com isso, iremos descontar a espessura total da barra e teremos o raio interno, e depois somaremos metade da espessura da barra (que é o raio dela) para termos o exato raio de curvatura do sistema, sendo assim teremos que:

Substituindo na nossa deformação teremos que:

E substituindo na nossa fórmula de tensão teremos que: