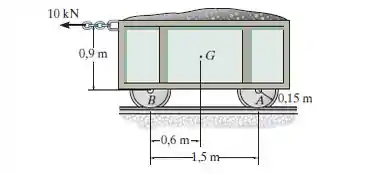
O vagão de mina e seu conteúdo possuem massa total de 6 Mg e centro de gravidade em . Se o coeficiente de atrito estático entre as rodas e os trilhos é quando as rodas estão travadas, determine a força normal que atua nas rodas da frente em e nas rodas de trás em quando os freios em e estão travados. O vagão se move?
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar se o vagão se move quando é aplicado uma força de . Em outras palavras, precisamos comparar a força de atrito máximo que podem atuar nas duas rodas da frente e nas duas de trás com a força de 10 kN.
Bom, a chave para resolvermos esta questão está no diagrama de corpo livre do vagão. Então, temos o seguinte diagrama:
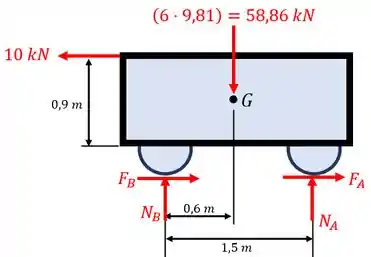
Agora vamos aos cálculos!
Passo 2
Vamos começar determinando a força normal atuante nos pontos e .
Para isto, vamos desconsiderar que o vagão está sendo puxado pela força de . Consequentemente, não temos forças de atrito e .
Logo, temos apenas o peso do carrinho e essas duas forças normais! Então, utilizando as equações de equilíbrio, temos:
Resolvendo o sistema acima obtemos e .
Passo 3
Agora que temos as forças normais, vamos calcular a força de atrito máximo em cada roda. Isto é, as forças de atrito que mantêm o vagão na iminência de se movimentar. Começando pelas rodas da frente, temos:
Já para as rodas de trás, temos:
Então, como a soma das duas forças de atrito é maior que a tração na corrente, isto é,
Podemos afirmar que o vagão está parado!
E assim finalizamos a questão!
Resposta
O vagão está parado