A parte da máquina é sustentada por uma dobradiça sem atrito em e uma cunha de em . Sabendo que o coeficiente de atrito estático nas superfícies da cunha é , deteremine a força necessária para mover a cunha, a correspondente componente da reação em .
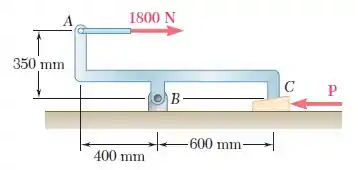
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
De cara podemos descobrir :
Logo:
Passo 2
Analisando o diagrama de corpo livre de temos:
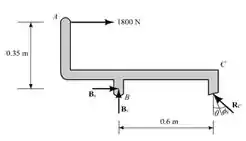
Fazendo o somatório de momento no ponto , temos:
Resolvendo, temos que:
Passo 3
Analisando o diagrama da cunha, temos que:
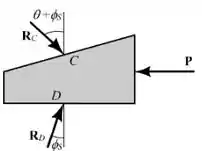
Podemos observar que as forças formam um triângulo. Podemos representa-lo assim:
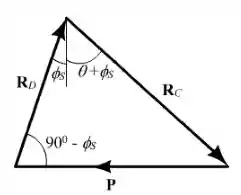
Aplicando a lei dos senos, temos que:
Substituindo os valores conhecidos, temos que:
Logo:
Que é a força necessária para mover a cunha.
Passo 4
Considerando a parte , temos que:
Da análise vertical, temos: