Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 72
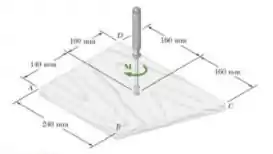
Um binário M de intensidade 18 N.m é aplicado no cabo de uma chave de fenda para apertar um parafuso em um bloco de madeira. Determine a intensidade das duas menores forças horizontais que são equivalentes a M, se estas forem aplicadas (a) nos cantos de A e D, (b) nos cantos de B e C, e (c) em qualquer lugar do bloco.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que tem essa chave e ela gera um momento binário. Mas se aplicarmos forças em 2 pontos da placa, essas forças podem ser equivalentes ao momento M. O que o enunciado quer saber é a menor intensidade dessas 2 forças, pro caso de diferentes pontos de aplicação.
Só vamos lembrar de uma coisinha antes de começar. Momento é força vezes a distância. Então, se a gente quer a menor força, pra resultar num mesmo momento, o nosso interesse é encontrar a maior distância. Bora ver em cada caso!
Passo 2
Ok, nosso primeiro passo vai ser achar a intensidade das forças quando elas são aplicadas em A e D. Como queremos a força mínima, vamos considerar que essas forças sejam perpendiculares à AD. Desse jeito, o momento fica assim:
Passo 3
Bom, para calcular a força entre B e C, vamos calcular a distância entre eles e, em seguida, a força.
Passo 4
Agora, pro item c, o enunciado não especificou o local das forças, então a gente pode colocar em qualquer lugar! Mas vamos lembrar que queremos as menores forças, então a gente precisa colocar elas duas nos 2 pontos da placa com a maior distância entre si. Esses são os pontos A e C.
De novo, vamos começar calculando a distância entre A e C e, depois, o valor das forças. Bora!