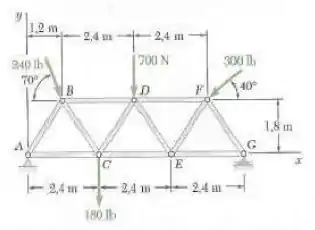
Uma treliça sustenta a carga mostrada na figura. Determine a força equivalente que atua sobre a treliça e o ponto de interseção da sua linha de ação com uma linha, que passa pelos pontos e .

Agora teremos o seguinte arranjo:

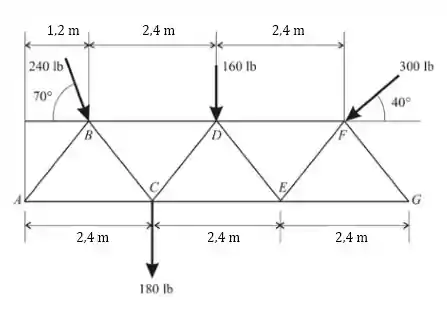
Analisando o diagrama podemos fazer o somatório das forças. Analisando as forças horizontais, temos que:

indica a resultante das forças horizontais que agem na treliça. Observe que o sinal foi negativo, o que indica que a direção da resultante é para o lado esquerdo.

Faremos agora o somatório de forças em verticais, temos que:

indica a resultante das forças verticais que agem na treliça. Observe que o sinal foi negativo, o que indica que a direção da resultante é para o lado baixo.

Como temos a resultante vertical e horizontal, podemos obter a reação resultante a partir do teorema de Pitágoras. O arranjo das reações ficou assim:

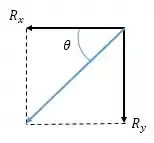
Calculando a resultante, temos:

Substituindo os valores, temos:

Podemos determinar também, o ângulo que indica a direção de .

Portanto:

Também nos é pedido para determinar o ponto de interseção da linha de ação dessa força resultante com a linha que liga o ponto ao ponto .

Para isso, vamos calcular o somatório de momentos no ponto . Temos que:

Temos então que:

Este resultado indica que o momento resultante causado pelas forças na treliça está no sentido horário.

Para determinar o ponto de interseção no segmento , vamos utilizar a relação de que o produto entre uma força que é perpendicular a um segmento é igual ao momento. Portanto:

Portanto a linha de ação da força passa a à direita do ponto .