Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 140

Uma cunha de peso desprezível é forçada entre dois blocos e de que repousam em uma superfície horizontal. Sabendo que o coeficiente de atrito estático em todas as superfícies de contato é , determine a menor força necessária para iniciar o movimento da cunha se os blocos são igualmente livres para mover, se o bloco está aparafusado na superfície horizontal.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Analisando a cunha, temos que:

De cara podemos descobrir :

Logo:

Passo 2

Analisando o diagrama de corpo livre podemos observar que as forças podem ser estudadas como um triângulo:

Aplicando a lei dos senos, temos:

Resolvendo, temos que:

Passo 3

Para determinar a menor força necessária para iniciar o movimento da cunha, temos que:

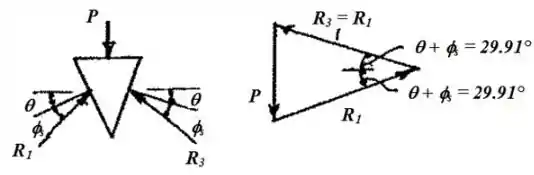
Como há simetria entre as reações e , temos que:

Substituindo os valores, temos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

56- O grampo está sendo usado para prender dois painéis enquanto a cola entre eles cura. Que torque M deve ser aplicado a manopla do parafuso para produzir uma compressão de 400N entre os painéis? O p

55- Calcule a força para a direita P ' que removeria a cunha de sob a porta do Prob. 6/54. Assuma que o canto A não desliza em seu calculo de P ' , mas depois verifique essa suposição o coeficiente de

O batente da porta de 10 ° é inserido com uma horizontal para a direita força de 30l b . Se o coeficiente de estática o atrito para todas as superfícies é μ s = 0,20 , determine os valores N U e N L d

Calcule o momento M ' que deve ser aplicado a alça do espaço do Prob. 6 / 70 para retirar a cunha e abaixar a carga de 100k g .

O pino cônico 2 ∘ é forçado em um orifício cônico correspondente no bloco fixo com uma força P = 400 N. Se a força necessária para remover o pino (com P = 0) é P '= 300 "" N , determina o coeficiente