Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 195
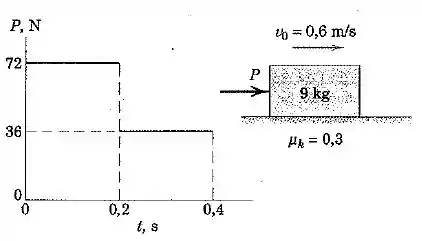
O bloco de está se deslocando para a direita com uma velocidade de sobre uma superfície horizontal quando uma força é aplicada a ele no instante de tempo . Calcule a velocidade do bloco quando . O coeficiente de atrito dinâmico é .
Passo 1
Vamos analisar a soma das forças que agem sobre o bloco na direçao horizontal:
E pelo teorema do impulso, podemos escrever a seguinte expressão:
Passo 2
Nosso primeiro passo é calcular essa integral:
A primeira integral é simplesmente a área do gráfico que foi dado no enunciado:
E a segunda é tranquila de calcular:
E então substituindo na fórmula de cima:
Resposta
A velocidade final do bloco é .
Exercícios de Livros Relacionados
O carrinho B , de 10k g , está apoiado em roletes de dimensão desprezível. Se uma maleta A de 5k g é lançada horizontalmente sobre o carrinho a 3m / s quando ele está em repouso, determine o tempo t e
A rampa de rolagem livre tem massa de 60k g . A caixa, cuja massa é 40k g é loberada do repouso em A , determine a distância que a rampa se move quando a caixa desliza 4,5m rampa abaixo até a base B .
145. Se a corrente é abaixada a uma velocidade constante, determine a reação normal exercida sobre o solo como função do tempo. A corrente tem massa de 10 kg/m e um comprimento total de 6m.
134. O caminhão tem massa m 0 e é usado para rebocar a corrente lisa que tem um comprimento total l e massa por unidade comprimento m ´ . Se a corrente está originalmente empilhada, determine a força
141. A escavadeira carrega inicialmente 10 m 3 de areia com uma densidade de 1520 kg/ m 3 . A areia é descarregada horizontalmente através de uma portinhola P, de 2,5 m 2 , a uma taxa de 900 kg/s, med