Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 199
O superpetroleiro tem um deslocamento (massa) total de toneladas métricas (uma tonelada métrica é igual a ) e está parado na água quando o rebocador começa a puxar. Se uma tração constante de é desenvolvida no cabo do rebocador, calcule o tempo necessário para levar o navio-tanque a uma velocidade de nó a partir do repouso. Nessa baixa velocidade, a resistência do casco ao movimento através da água é muito pequena e pode ser desprezada. ( nó )
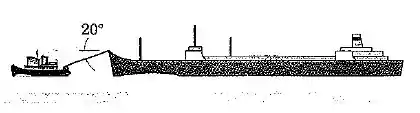
Passo 1
Nosso objetivo é provocar uma variação no momento linear do superpetroleiro:
E adicionamos o fator para converter a velocidade para metros por segundo;
Passo 2
Pelo teorema do impulso, sabemos que essa variação de momento depende da ação de uma certa força por um intervalo de tempo:
Nesse caso a força é constante , mas precisamos considerar apenas sua componente na direção da velocidade:
E em minutos, temos:
Resposta
São necessários minutos.