A porta de garagem suspensa é um painel retangular homogêneo de massa e é guiada por seus roletes nas extremidades, que correm nos trilhos mostrados (tracejados). Se a porta é liberada a partir do repouso na posição mostrada, determine a força exercida na porta por cada um dos roletes em e . Despreze qulquer atrito.
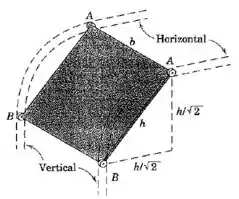
Passo 1
Vamos fazer um desenho que represente a vista lateral da porta, mostrando as forças e as acelerações que agem sobre o sistema:
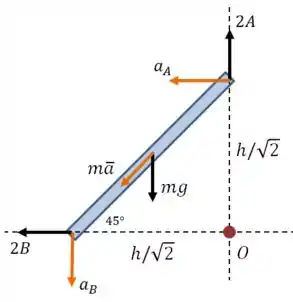
Onde deduzimos o ângulo de pelo dato de os dois “catetos” do triângulo serem iguais.
Vamos começar aplicando a segunda lei de Newton nas direções vertical e horizontal:
E na direção vertical:
Passo 2
Podemos escrever também uma equação de momentos em relação ao ponto :
E a única força que produz em relação a esse ponto é o peso, que está a uma distância perpendicular do ponto :
E o momento de inércia da placa retangular em relação ao centro de massa é tabelado:
Onde , que é exatamente a distância entre e o centro de massa da porta. Podemos simplificar um pouco essa equação:
Com isso ficamos com um ssitema de três equações:
Aqui ainda temos quatro variáveis desconhecidas para apenas três equações, então vamos precisar determinar alguma dessas variáveis antes de continuar.
Passo 3
Vamos escrever algumas relações para as acelerações de , e do centro de massa:
Onde a aceleração deve apontar na mesma direção de .
Além disso, pode ser determinada pela aceleração angular do sistema e a distância entre os dois pontos:
Então vamos representar isso vetorialmente:

E podemos usar o ângulo de para determinar alguns valores:
Além disso:
Então:
Passo 4
Agora vamos substituir essa informação no nosso sistema:
Começando pela primeira equação, para determinar a aceleração angular :
E agora vamos substituir na segunda equação para encontrar a força :
E podemos substituir a expresão que já determinamos para :
E finalmente vamos substituir na terceira para encontrar a força :
Resposta
As forças são e .