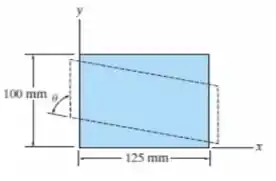
O bloco é feito de titânio . É submetido a uma compressão de ao longo do eixo , e sua forma sofre uma inclinação de Determine .

Queremos encontrar os valores de dado o quanto a barra foi comprimida e ao longo de qual eixo, além disso, temos o ângulo de inclinação que essa barra sofre. Devemos lembrar que cada um desses itens será calculado de uma forma diferente que é mostrada a seguir

• Para podemos utilizar a fórmula da tensão normal
• Para podemos relacionar com através do coeficiente de Poisson da seguinte forma
• Por fim, para vamos utilizar a tensão de cisalhamento e teremos

Onde

comprimento na direção sobrescrita;

Suplementar do ângulo de inclinação;

Coeficiente de Poisson para o Titânio (0.36 para o titânio do problema);

compressão sofrida pela barra;