Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 3.Problemas - Ex. 30
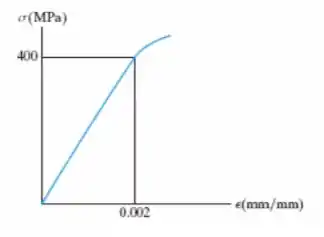
A figura mostra a porção elástica do diagrama tensão - deformação para um aço-liga. O corpo de prova do qual ela foi obtida tinha diâmetro original de e comprimento de referência de . Se uma carga for aplicada ao corpo de prova, determine o seu diâmetro de referência. Considere .
Passo 1
Oláaaa, querido!
Então, ele diz que um corpo de prova está sofrendo uma carga de . Ou seja, a força normal interna nele é essa.
Podemos supor que essa força tende a alongar o corpo de prova cilíndrico. Então se inicialmente ele tinha um comprimento de referência de , o comprimento de referência com ação da carga sobre o corpo de prova vai ser maior.
Bem, quando uma carga tende a alongar um corpo de prova cilíndrico, o diâmetro desse corpo de prova vai diminuir.
Aí o enunciado quer saber o comprimento de referência do corpo de prova e o diâmetro quando estamos com a carga aplicada. Bora ver como achar isso!
Passo 2
Primeiro, vamos calcular a tensão normal na haste. O enunciado já nos dá a carga axial e o diâmetro inicial da barra, logo, vamos substituir. Temos:
Substituindo:
Percebe que como a gente usou e , o resultado saiu em 😊
Passo 3
Percebe que a tensão que a gente achou é menor que a tensão de escoamento, então ainda estamos no regime linear e podemos aplicar a lei de Hooke para determinar a deformação do comprimento causada pela tensão normal, temos:
A gente não temo o módulo de elasticidade, mas do diagrama de tensão – deformação podemos encontrar o módulo de elasticidade que é o coeficiente angular da reta desenhada no gráfico, assim temos
Substituindo isso e a tensão normal na lei de Hooke, a deformação fica:
Passo 4
E assim, podemos determinar a mudança no comprimento do corpo de prova pela fórmula da deformação longitudinal. Temos:
Aí para saber o comprimento do corpo de prova com ação da carga, a gente soma esse alongamento ao comprimento inicial do corpo de prova:
Passo 5
Falta achar a variação de diâmetro, e assim o diâmetro com ação da carga. Como ele deu o coeficiente de Poisson , podemos relacionar a deformação longitudinal (ao longo do comprimento) com a deformação axial (mudança no diâmetro), através dessa expressão:
Já que temos a deformação longitudinal, vamos substituir aí e achar a radial:
Passo 6
E para que a gente quer essa deformação? Porque podemos usar o valor de para encontrarmos a variação do diâmetro. Podemos escrever a deformação axial assim:
Onde é a variação de diâmetro. Vamos isolar essa bonita:
Substituir o que a gente tem:
Aí o diâmetro com ação da carga vai ser o diâmetro inicial mais esse :