Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 3.Problemas - Ex. 34
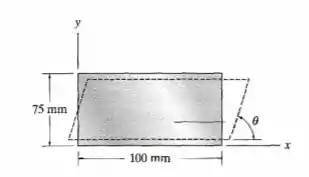
O bloco de borracha é submetido a um alongamento de ao longo do eixo , e suas faces verticais sofrem uma inclinação de modo que Determine as deformações . Considere .
Passo 1
Fala aí meus camaradas, como vocês estão? Prontos pra mais uma resolução?
Vamos lá, nós queremos encontrar as deformações . Só para lembrar elas equivales, respectivamente, as deformações em em e a deformação angular =D
Pois bem, vamos primeiramente deixar anotado aqui alguns dados fornecidos no enunciado de acordo com a notação que usaremos no problema, então, temos
Para resolver essa questão a gente tem que primeiro achar essas deformações e depois achar beleza? Vamos começar?
Passo 2
Para a tensão normal nós vamos ter que a deformação é igual à deformação específica vezes o comprimento :
Reformulando:
Como temos o valor de vamos ter o seguinte
Passo 3
Agora se liga só nisso aqui: a gente tem uma equação que relaciona as deformações no eixo e no eixo que é a do coeficiente de Poisson e ela é dada da seguinte forma
obs: Isso é a representação de quando a gente amassa uma massinha de modelar!! Quando a gente amassa ela na vertical ela não cresce na horizontal? Então é isso!! Por isso até que os sinais são invertidos.
Então vamos ter:
Passo 4
Por fim, para encontrarmos o valor da tensão de cisalhamento , vamos primeiramente converter nosso ângulo de graus para radianos, lembra como faz isso?
Tem problema não, vamos relembrar aqui fazendo uma regra de três simples, achou que não ia usar mais isso na universidade, né? Achou errado, meu brother e minha brother. Olha só como é simples
Multiplicando cruzado vamos ter:
Beleza, mas como vamos encontrar essa bendita tensão? Bem simples, só aplicar a seguinte fórmula
Substituindo nossos dados vamos ter
Pronto, acabamos mais um exercício com sucesso.