Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 22
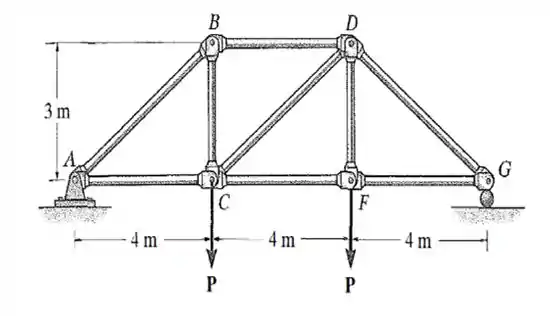
22. Consideramos que os elementos estruturais da treliça estão acoplados por pinos. Se o elemento estrutural BD for uma haste de aço de raio , determine a carga máxima que pode ser suportada pela treliça sem provocar flambagem no elemento estrutural.
Passo 1
Olá! Tudo bem?
Queremos saber o maior valor de para não haver flambagem em .
Bem! Como as extremidades das treliças estão acopladas por pinos, já sabemos que o seu fator de comprimento efetivo é igual a .
Vamos começar achando as rainhas da resistência dos materiais: as reações de apoio.
Podemos ver que as reações em e , respectivamente e , vão ser iguais em módulo a , mas em sentido oposto, apontando para cima. Por que? Por causa da simetria do carregamento.
E temos uns dados do aço-36 que são tabelados, então é melhor listar aqui
Vamos seguir!
Passo 2
Podemos começar achando a carga crítica. Já que a gente quer um carga limite para não haver flambagem, né?
Vamos então, usar a expressão da carga crítica para a flambagem.
Só que a nossa haste é um elemento circular de raio , que tem o momento de inércia vai ser dado por:
E ficamos com a fórmula modificada desse jeito:
O comprimento da haste é .
Falta apenas substituir os valores numéricos pertencentes a cada variável, de modo que chegamos até:
Passo 3
Vamos ver se essa carga não faria nossa estrutura sair do regime linear elástico:
Já que sabemos o valor da carga crítica , apliquemos então a outra velha e conhecida fórmula de tensão, dada pela divisão da força pela área em que ela atua:
Esse valor é menor do que a tensão admissível para o nosso aço , que é igual a Logo, está tudo certo com o resultado! E aquela vai ser mesmo nossa carga critica.
Passo 4
Voltando para a treliça, vamos achar , a força aixial no elemento em função de .
Como estamos trabalhando com o elemento estrutural , onde queremos a força atuante nesse trecho, o que acha de usarmos o método das seções para tentar descobrir nosso objetivo!? Vamos considerar a seção , como ponto de análise:
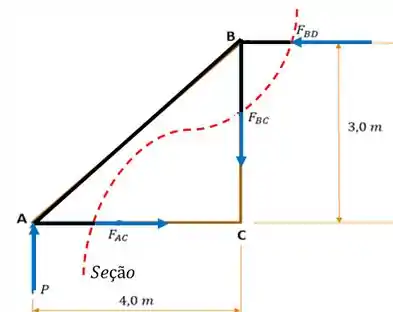
Aí como se a gente tivesse cortado nossa treliça numa seção que corta ao mesmo tempo a barra , depois a e depois a .
Agora, o que temos que fazer é o somatório das forças e momentos no nosso elemento , para ver se conseguimos tirar as relações que queremos:
Fazendo primeiro, o somatório dos momentos no ponto :
E depois, fazendo o somatório das forças em , chegamos à:
Substituindo isso na expressão que a gente achou pelo momento:
Prontinho! Temos em função de .
Passo 5
Mas ainda não acabou! Obtemos no , que e coincidentemente já sabemos o valor de que nada mais é do que a carga crítica . Por que? Porque a gente quer o valor limite para que não faça o elemento sofrer flambagem. Ou seja,
Assim, obtemos nossa resposta como o resultado da expressão abaixo: