Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas de Revisão - Ex. 123
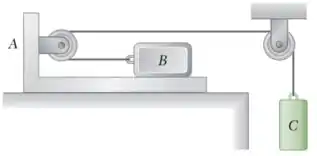
Um bloco B de 6 kg descansa em um suporte A, como mostrado na figura. Os coeficientes de atrito são = 0,30 e = 0,25 entre o bloco B e o suporte A e não há atrito na roldana ou entre o suporte e a superfície horizontal. (a) Determine a maior massa do bloco C se o bloco B não desliza sobre o suporte A. (b) Se a massa do bloco C é 10% maior que a resposta encontrada em a, determine a aceleração de A, B e C.
Passo 1
Cinemática: Deixando e como coordenadas horizontais de A e B medidas de uma linha vertical fixa a esquerda de A e B. Deixando ser a distância que o bloco C está embaixa da polia. Note que aumenta quando C se covimenta para baixo. Observe a figura.
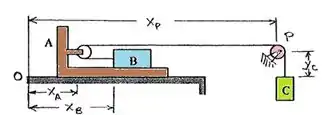
O comprimento do cabo L é fixo.
Diferenciando e notando que
(1)
Aqui, e são positivos para a direita, e é positiva para baixo.
Passo 2
Cinética. Deixando T ser a tensão no cabo e ser a força de fricção entre o bloco A e B. Os diagramas de corpo livre são:
Bracket A:
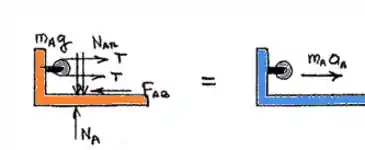
Bloco B:
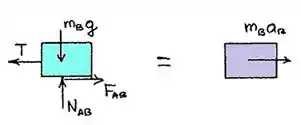
Bloco C:
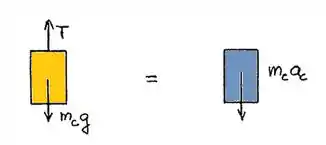
Bracket A:
(2)
Bloco B:
(3)
ou
Bloco C:
(4)
Adicionando Eqs. (2),(3), e (4), e transpondo,
(5)
Subtraindo Eq. (4) da Eq. (3) e transpondo,
(6)
Passo 3
(a)Sem deslizamento entre A e B.
Da Eq. (1),
Da Eq. (5),
Fara o deslizamento impedido,
Substituindo na EQ. (6),
Resolvendo para ,
Passo 4
(b) aumentado em 10%.
Desde que o deslizamento ocorre,
Eq. (6) se torna
ou
(7)
Com os dados numericos, Eq. (5) se torna
(8)
Resolvendo Eqs. (1),(7) e (8) temos