Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 51

O disco tem uma massa de 15 kg. Se ele é solto do repouso quando θ = 30 ° , determine o ângulo máximo θ de repique após ele colidir com a parede. O coeficiente de restituição entre o disco e parede é e = 0,6 . Quando θ = 0 ° , o disco está pendurado de tal maneira que ele apenas toca a parede. Despreze o atrito no pino C.

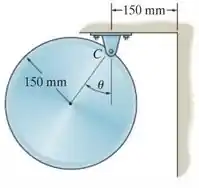
Passo 1

Para o movimento ocasionado pela soltura do disco até o choque com a parede deve-se aplicar a equação da conservação da energia mecânica. Como ilustrado no esquema abaixo, tomando como referência o momento em que o disco toca a parede, quando θ = 30 ° o disco está em repouso ea uma altura y G 1 , em seguida, ao tocar a parede terá velocidade angular ω 2 com altura y G 2 nula.

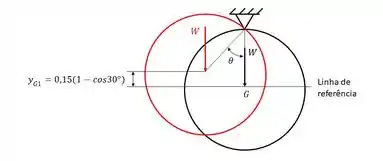
Logo,

T 1 + V 1 = T 2 + V 2

1 2 m v 1 2 + 1 2 I G ω 1 2 + W y G 1 = 1 2 m v 2 2 + 1 2 I G ω 2 2 + W y G 2

Como,

T = 1 2 m v 1 2 + 1 2 I G ω 1 2 = 1 2 3 2 m R 2 ω 2

Então,

1 2 3 2 m R 2 ω 1 2 + W y G 1 = 1 2 3 2 m R 2 ω 2 2 + W y G 2

0 + 15 9,81 0,15 1 - c o s 30 ° = 1 2 3 2 15 0,15 2 ω 2 2 + 0

ω 2 = 3,418   r a d / s

Passo 2

Ao tocar na parede, deve-se calcular a nova velocidade angular do disco através da seguinte equação:

e = ( v B ) 2 - ( v A ) 2 ( v A ) 1 - ( v B ) 1

0,3 = 0 - ( - 0,15 ω 3 ) 3,418 ( 0,15 ) - 0

ω 3 = 2,0508   r a d / s

Passo 3

O ângulo θ pode ser obtido relacionando as velocidades de colisão e pós-colisão através da equação da conservação da energia.

T 3 + V 3 = T 4 + V 4

1 2 3 2 m R 2 ω 3 2 + W ( y G ) 3 = 1 2 3 2 m R 2 ω 4 2 + W ( y G ) 4

1 2 3 2 15 0,15 2 2,0508 2 + + 0 = 0 + 15 9,81 0,15 1 - c o s θ

θ = 17,9 °

Resposta

O ângulo máximo θ de repique após ele colidir com a parede é igual a 17,9°.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A balia jubarte de 5,5 Mg está encalhada na praia, devido à variação na maré. Em um esforço para resgatar a baleia, um barco rebocador de 12 Mg é utilizado para libertá-la empregando uma corda inexten
A caixa de 100 kg é içada pelo motor M . O motor excerce no cabo uma força T = 200 t 1 / 2 + 150N onde t está em segundos. Se a caixa parte do repouso no solo, determine a velocidade da caixa quando t
A força atuando sobre um projétil que tem massa m , enquanto este passa horizontalmente pelo cano do canhão é F = C sen ⁡ ( π t / t ' ) . Determine a velocidade do projétil quando t = t ' . Se o projé
A prancha rígida de 15k g é atingida pela cabeça do martelo H de 7,5k g . Imediatamente antes do impacto, o martelo é seguro livremente e tem uma velocidade vertical de 22,5m / s . Se o coeficiente de
O sino de 150 kg está em repouso na posição vertical quando é atingido pela viga de madeira de 37,5 kg, suspensa por duas cordas de igual comprimento. Se a viga é solta do repouso em θ = 45 ° , determ