Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 11

Um bloco de 10 kg é colocado sobre o plano inclinado como mostrado na figura, as forças de 30 e 75N atuam paralelas as arestas AB e AC, respectivamente. Se ele está inicialmente em repouso, determinar sua velocidade quando t=3s e sabendo que o coeficiente de atrito cinético entre o bloco e a superfície é µc=0,2.

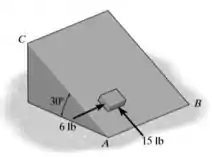
Passo 1

Fazendo o DCL no bloco, temos que:

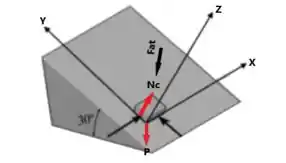
Fazendo as considerações necessárias para este DCL, temos que o eixo Z é perpendicular ao plano de deslizamento do bloco, ou seja, o bloco está sendo empurrado apenas no plano x-y. A força de atrito Fat, está agindo apenas na superfície de deslizamento, ou seja, apenas em x-y. a força peso P do bloco age a 30° de inclinação de Z e apenas no plano y-z.

Passo 2

Com isso, teremos para Z:

m * v z 1 + ∑ ∫ t 1 t 2 F z d t = m * v z 2

Portanto teremos:

10 * 0 + N c * 3 - P * c o s 30 ° * 3 = 10 * 0

Logo:

N c = P * c o s 30 ° = m . g * c o s 30 ° = 10 * 9,81 * c o s 30 ° = 84,96 N

Para o plano X-Y, temos que:

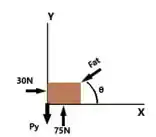
Onde o movimento do bloco será na direção da força de atrito Fat, porém em sentido oposto, com isso, na direção Y, temos que:

m * v y 1 + ∑ ∫ t 1 t 2 F y d t = m * v y 2

Assim:

10 * 0 + 75 * 3 - F a t * s i n θ * 3 - P * s i n 30 ° * 3 = 10 * v * s i n θ

0 + 225 - µ c * N c * s i n θ * 3 - m * g * s i n 30 ° * 3 = 10 * v * s i n θ

225 - 0,2 * 84,96 * s i n θ * 3 - 10 * 9,81 * s i n 30 ° * 3 = 10 * v * s i n θ

s i n θ 10 * v + 50,98 = 77,85                     ( 1 )

Para o eixo X, temos:

m * v x 1 + ∑ ∫ t 1 t 2 F x d t = m * v x 2

10 * 0 + 30 * 3 - F a t * c o s θ * 3 = 10 * v * c o s θ

0 + 90 - µ c * N c * c o s θ * 3 = 10 * v * c o s θ

90 - 0,2 * 84,96 * c o s θ * 3 = 10 * v * c o s θ

Isolando vx2, temos:

c o s θ 10 * v + 50,98 = 90                     ( 2 )

Dividindo (1) por (2), temos:

s i n θ 10 * v + 50,98 c o s θ 10 * v + 50,98 = 77,85   90                

Então:

t g θ = 0,865

Com isso:

θ = a r c t g 0,865 = 40,86 °

Aplicando θ=40,86° em qualquer uma das equações, teremos que:

v = 6,8 m / s

Resposta

O bloco irá se deslocar com uma velocidade de 6,8m/s em uma direção com 40,86° de inclinação com relação ao eixo X.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O módulo de pouso lunar de 17,5t com centro de massa G tem um raio de giração de 1,8m em relação a G . O módulo é projetado para pousar na superfície lunar com uma velocidade vertical de queda livre d
Uma professora de dinâmica com 55k g está demonstrando os princípios da quantidade de movimento angular para sua classe. Ela fica de pé sobre uma plataforma que gira livremente com seu corpo alinhado
Cada uma das duas barras uniformes A de 300m m possui uma massa de 1,5k g e é articulada em sua extremidade à base B que está girando. A base com 4k g tem um raio de giração de 40m m e está inicialmen
A roda de 30k g tem um raio de giração em relação a seu centro de 75m m e está girando no sentido horário na taxa de 300r p m , quando é liberada no plano inclinado sem velocidade em seu centro O . En
A caixa de 100 kg é içada pelo motor M . Se a velocidade da caixa aumenta uniformemente, de 1,5 m/s para 4,5 m/s em 5 segundos, determine a tração desenvolvida no cabo durante o movimento.