Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 9
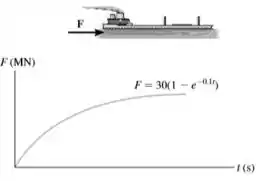
O navio petroleiro tem uma propulsão horizontal produzida por sua hélice em função do tempo como mostrado no gráfico e tem uma massa de 130Gg. Determinar sua velocidade quando t=10s. Desprezar a resistência da água.
Passo 1
Fazendo uma análise na direção horizontal, percebemos que a única força existente será a da propulsão causada pela hélice, que varia com o tempo, disso podemos tirar nossos rumos para a resolução do problema.
Passo 2
Sabemos que
Portanto teremos:
Resposta
Após 10 segundos de tempo, o navio estará a uma velocidade de 0,8489m/s. O que pode ser explicado pela sua grande massa, o que faz o navio demorar pra atingir altas velocidades.
Exercícios de Livros Relacionados
Cada uma das duas barras tem uma massa m e um comprimento l, e repousam sobre o plano horizontal liso. Se um impulso I é aplicado em um ângulo de 45° com uma das barras no meio do comprimento, como mo
O poste uniforme tem uma massa de 15 kg e cai do repouso quando θ = 90 ° . Ele bate na aresta em A quando θ = 60 ° . Se o poste então começa a pivotar em torno desse ponto após o contato, determine a
Uma bola tendo uma massa de 8 kg e velocidade inicial v 1 = 0,2m / s rola sobre uma depressão de 30 mm de comprimento. Supondo que a bola rola pelas arestas de contato primeiro A, depois B, sem desliz
O centro O da roda tem uma velocidade v 1 = 2 m / s para cima na inclinação de 10 % no instante de tempo t = 0 . Encontre a velocidade v 2 da roda quando t = 6s . A roda tem um raio de giração de 90m
Uma força horizontal constante P é aplicada ao centro O do disco circular uniforme de massa m por meio do garfo leve como mostrado. O disco parte do repouso e rola por t segundos sem deslizar sobre a