Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 14
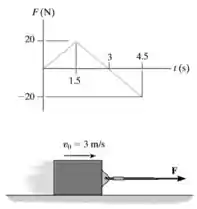
Um bloco liso de 2kg se move para a direita com uma velocidade inicial de 3m/s, quando a força F, que varia com o tempo, é aplicada. Determinar a velocidade do bloco quando t=4,5s.
Passo 1
Sabemos que o impulso é
Portanto, teremos que o impulso será, neste caso, a soma das áreas 1, 2 e 3 demonstradas abaixo.
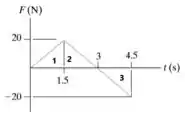
Logo:
Passo 2
Temos que:
Sabendo que vx1, quando t=0 é 3m/s e que a massa do bloco é de 10kg, considerando rambém que não haja atrito pelo fato de ser um bloco liso, temos:
Resposta
Após 4,5 segundos de aplicação da força variada F, a velocidade do bloco liso será de 4,5m/s.
Exercícios de Livros Relacionados
A pressão da água em C é 300k N / m 2 . Se a água flui para fora do cano em A e B , com velocidades v A = 3,6m / s e v B = 7,5m / s , determine as componentes da força horizontal e vertical exercidos
As rodas do carro de 1,5 Mg geram a força de tração F descrita pelo gráfico. Se o carro parte do repouso, determine a sua velocidade quando t = 6s.
Se o coeficiente de atrito cinético entre a caixa de 750N (m≈75 kg) e o solo é μ k = 0,2, determine a velocidade da caixa quando t=4s. A caixa parte do repouso e é arrastada pela força de 500 N.
O veículo de tração nas quatro rodas de 2,5 Mg puxa um reboque de 1,5 Mg. A força de tração desenvolvida nas rodas é de Fd = 9 kN. Determine a velocidade do veículo em 20 segundos, partindo do repouso
O bloco A, de 50N (≈ 5 kg), atinge uma velocidade de 0,3 m/s em 5 segundos, partindo do repouso. Determine a tração no cabo e o coeficiente de atrito cinético entre o bloco A e o plano horizontal. Des