Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 7

Os foguetes de 1,5MG fornecem um impulso como mostrado no gráfico, determinar a velocidade máxima atingida pelos veículos sobre o trilho desprezando o atrito e a massa perdida devido ao consumo de combustível.

Passo 1

Sabemos que:

I = ∫ F d t

Portanto, o impulso será a área total representada pela força T em função do tempo. Por isso podemos calcular a área e assim teremos o valor do impulso causado pelos foguetes.

Sabendo isso, podemos calcular as áreas das formas geométricas 1, 2, 3, 43 5 demonstradas abaixo:

Logo teremos que:

I = ∑ n = 1 5 A r e a n = a r e a 1 + a r e a 2 + a r e a 3 + a r e a 4 + a r e a 5

Com isso:

I = 30 * 0,5 + 60 * 1 - 0,5 + 90 * 1,5 - 1 + 60 * 2 - 1,5 + 30 * ( 2,5 - 2 )

I = 135 K N . s = 135000 N . s

Passo 2

Fazendo um DCL no foguete, temos:

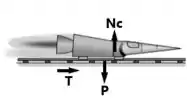
Portanto, teremos que:

m * v 1 + ∑ ∫ t 1 - t 2 T d t = m * v 2

Sabemos também que a velocidade inicial é 0, logo, poderemos calcular a velocidade máxima como:

1,5 * 10 3 * 0 + 135000 = 1,5 * 10 3 * v m á x

v m á x = 135000 1,5 * 10 ³ = 90 m / s

Resposta

Desprezando o atrito e a perda de massa pelo consumo de combustivel, o foguete pode chegar a uma velocidade máxima de 90m/s, pelo impulso dado no gráfico.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A bola de 0,5 kg atinge o solo áspero e ricocheteia com as velocidades mostradas. Determine a intensidade do impulso que o solo exerce sobre a bola. Suponha que a bola não desliza quando atinge o solo
O motor de 25 kg exerce uma força de F =(20t2) N sobre o cabo, onde t é dado em segundos. Determine a velocidade da caixa onde t=4s Os coeficientes de atrito estático e cinético entre a caixa e plano
Um bloco de 2,5 kg inicia a uma velocidade de 3m/s em um aclive liso de 45°, determinar o tempo que o bloco se moverá aclive acima até parar.
É dada uma velocidade ascendente de 1,5m/s quando t=0,3s ao elemento de combustível de um reator nuclear com um peso de 3000N que está suspenso em H, na posição vertical e inicialmente em repouso. Cal
O gráfico mostra a força reativa vertical entre solo e sapato como uma função do tempo, onde o primeiro pico representa a força reativa com relação ao calcanhar e o segundo com relação à parte frontal