Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 102
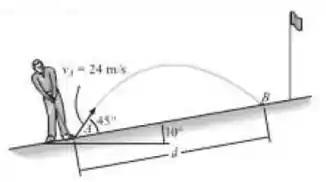
Uma bola de golfe é batida com uma velocidade de , como mostrado. Determine a distância d medida do lançamento até o ponto B.
Passo 1
Temos um problema de lançamento oblíquo com um plano inclinado. O ponto complicado nesta questão é trabalhar com este plano inclinado. Precisamos decompor a velocidade na direção e , e depois utilizar as relações de posição para estes eixos. Para podermos fazer esta decomposição, precisamos determinar o ângulo formado pela velocidade e o eixo . Este ângulo é exatamente ! Consequentemente, a decomposição da velocidade é:
Agora que sabemos o valor da velocidade na direção dos eixos e , nos falta relacionar a posição do ponto B com o valor de d. Utilizando trigonometria, temos:
Agora que temos as coordenadas dos pontos e a sua velocidade decomposta, já passamos pela parte mais difícil! Precisamos utilizar agora as equações da cinemática para resolvermos o nosso problema! Só tomem cuidado para não errarem conta!
Passo 2
Vamos começar analisando o movimento da bola na direção do eixo . Como a mesma não está sujeita a nenhuma aceleração nesta direção, teremos:
Conseguimos uma relação entre o tempo e a distância d.
Passo 3
Vamos analisar o movimento da mesma no eixo . Nesta direção, ela está sujeita a ação da gravidade. Portanto, temos a seguinte equação da cinemática:
Lembrando que , temos:
Resolvendo esta equação, obtemos e . Como o valor de é diferente de zero, temos então: