Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 122
A um bloco de madeira de de seção transversal, são pregadas quatro pranchas de seção transversal . Pede-se:
- Determinar a tensão compressiva no bloco, causada por uma carga axial centrada de .
- A prancha 1
- A prancha 1 e 2
- A prancha 1, 2 e 3
- Todas as pranchas
Sabendo-se que, em cada um dos casos que se seguem, a carga axial de é aplicada no centro da madeira 100 x 100 mm, determinar a maior tensão de compressão no bloco, se são removidas:
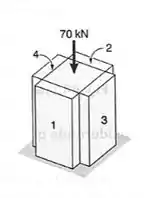
Passo 1
Nosso objetivo é determinar a máxima tensão de compressão, e sabemos que a fórmula é dada por:
Para o item A) deseja-se saber a tensão normal que age na nossa prancha, olhado o perfil teremos que:
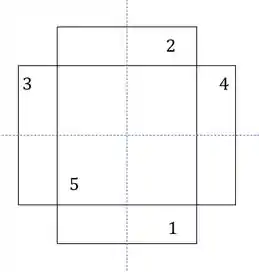
Como a carga de está centrada no perfil 5, e o nosso perfil é simétrico nas duas direções, com isso teremos que o momento fletor será zero, já que não temos excentricidade, sendo assim a nossa fórmula é dada por:
Calculando a área teremos que:
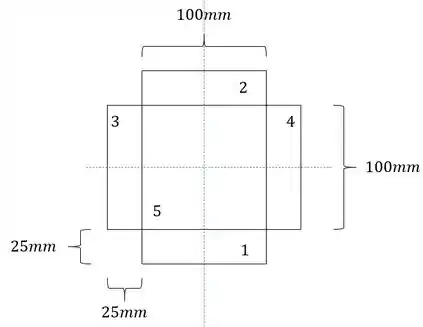
Substituindo teremos que:
Passo 2
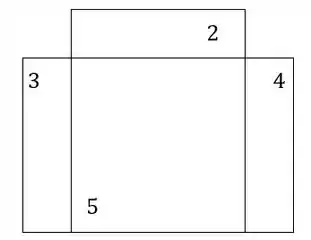
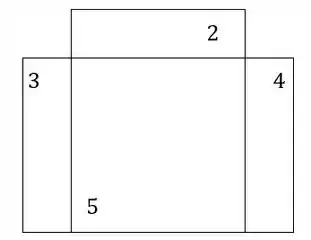
Para o item B) faremos o mesmo cálculo, mas iremos tirar a prancha 1, sendo assim teremos que a nossa seção será:
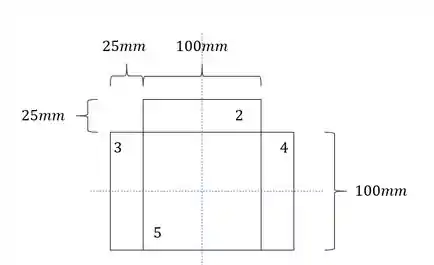
Como a seção é assimétrica, precisamos determinar a LN.
- Vamos dividir em seções mais simples, e numerar elas:
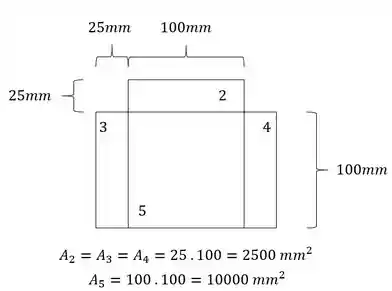
- As áreas são:
- Em terceiro, precisamos determinar uma origem, porque vai ser com relação com essa origem que vamos determinar a distância dos centroides de cada um dos elementos mais simples. Eu geralmente uso a base do elemento como origem, sendo assim teremos que:
- Por fim precisamos usar a seguinte fórmula para determinar a LN, sendo assim teremos que:
-
Para ele precisamos fazer a seguinte relação.
- Numeração das regiões
- Área das regiões
- Distância do centroide das áreas até a LN – aqui que vamos precisar da nossa LN
- Momento de inércia de cada região
Olha como esse macetinhos nos ajuda bastante.
- positivo e negativo
- Vamos dividir em seções mais simples, e numerar elas:
- As áreas são:
- Em terceiro, precisamos determinar uma origem, porque vai ser com relação com essa origem que vamos determinar a distância dos centroides de cada um dos elementos mais simples. Eu geralmente uso a base do elemento como origem, sendo assim teremos que:
- Por fim precisamos usar a seguinte fórmula para determinar a LN, sendo assim teremos que:
-
Para ele precisamos fazer a seguinte relação.
- Numeração das regiões
- Área das regiões
- Distância do centroide das áreas até a LN – aqui que vamos precisar da nossa LN
- Momento de inércia de cada região
Olha como esse macetinhos nos ajuda bastante.
- positivo e negativo
Calculando a área temos que:
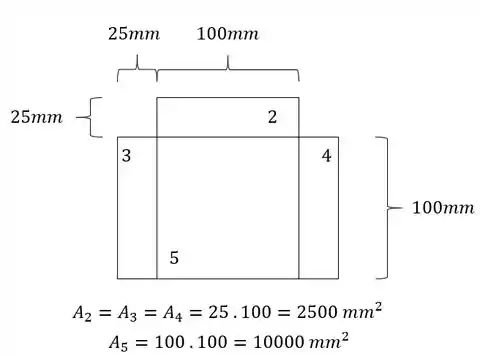
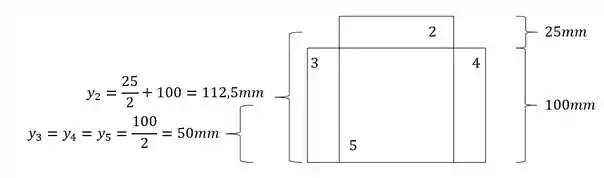
Com isso teremos que:
Substituindo teremos que:
E assim temos que:
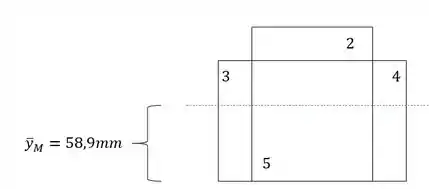
Passo 3
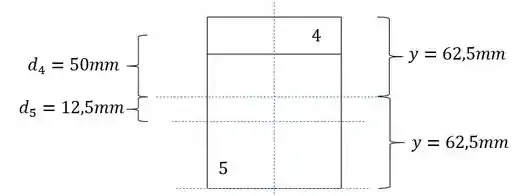
Vamos definir primeiro o momento de inércia e y teremos que:
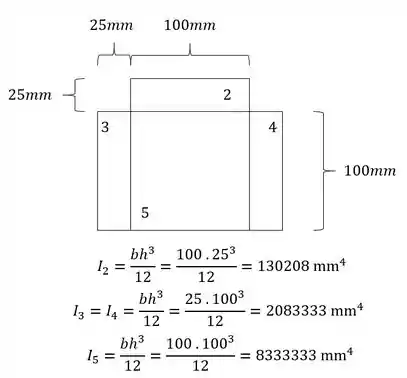
Agora para determinarmos o momento de inércia, precisamos fazer a seguinte conta:
Mas temos que lembrar que precisamos usar os valores de inercia da região 6 como negativa, sendo assim temos que:
Agora só precisamos determinar os valores de y, sendo assim teremos que ver o próximo passo.
Passo 4
Tendo o valor de y precisamos usar a tensão, sendo assim teremos que:
E para calculo de momentos fletores temos que usar a excentricidade :
Como o momento está na direção negativa, devemos usar os valores de y inferirores para temros o máximo de tesnões de compressão, sendo assim teremos que:
Passo 5
Para o item C) deseja-se saber a tensão normal que age na nossa prancha, olhado o perfil teremos que:
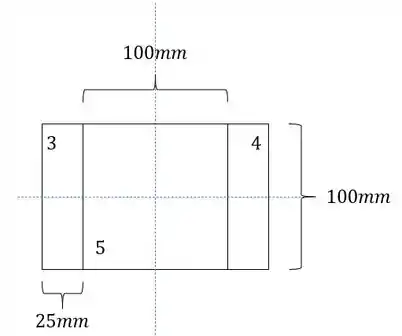
Como a carga de está centrada no perfil 5, e o nosso perfil é simétrico nas duas direções, com isso teremos que o momento fletor será zero, já que não temos excentricidade, sendo assim a nossa fórmula é dada por:
Calculando a área teremos que:
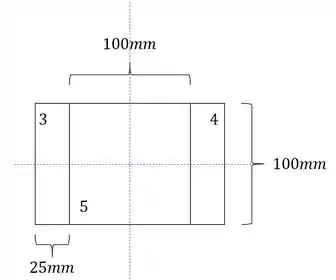
Substituindo teremos que:
Passo 6
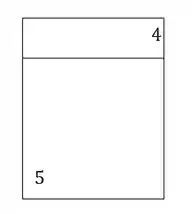
Para o item d) faremos o mesmo cálculo, mas iremos tirar a prancha 1,2 e 3, sendo assim teremos que a nossa seção será:
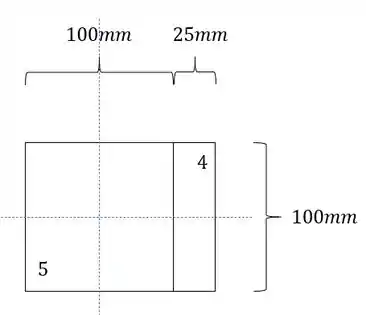
Se girarmos a seção para facilitar a visualização do cálculo, teremos que:
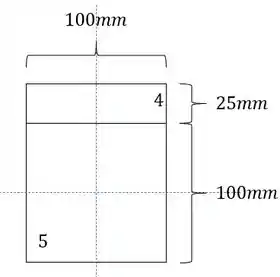
Como a seção é assimétrica, precisamos determinar a LN.
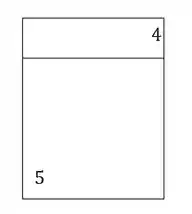
Calculando a área temos que:
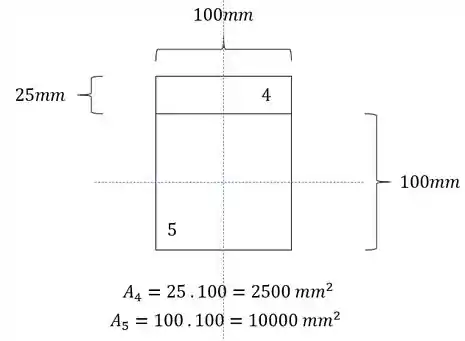
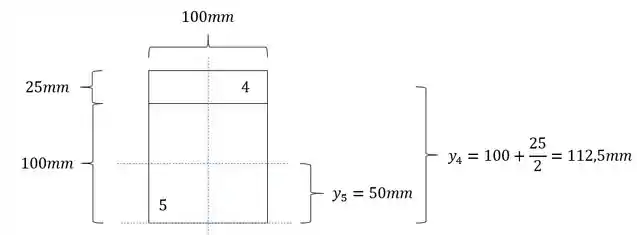
Com isso teremos que:
Substituindo teremos que:
E assim temos que:
Passo 7
Vamos definir primeiro o momento de inércia e y teremos que:
Agora para determinarmos o momento de inércia, precisamos fazer a seguinte conta:
Mas temos que lembrar que precisamos usar os valores de inercia da região 6 como negativa, sendo assim temos que:
Agora só precisamos determinar os valores de y, sendo assim teremos que ver o próximo passo.
Passo 8
Tendo o valor de y precisamos usar a tensão, sendo assim teremos que:
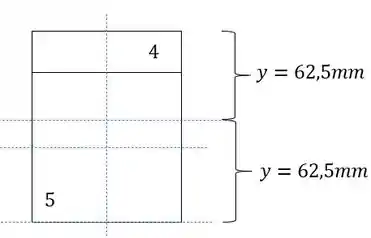
E para calculo de momentos fletores temos que usar a excentricidade :
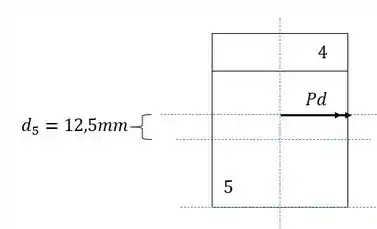
Como o momento está na direção negativa, devemos usar os valores de y inferirores para temros o máximo de tesnões de compressão, sendo assim teremos que:
Passo 3
Para o item e) deseja-se saber a tensão normal que age na nossa prancha, olhado o perfil teremos que:
Como a carga de está centrada no perfil 5, e o nosso perfil é simétrico nas duas direções, com isso teremos que o momento fletor será zero, já que não temos excentricidade, sendo assim a nossa fórmula é dada por:
Calculando a área teremos que:
Substituindo teremos que: