Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 154a

A carga de 120   k N pode ser aplicada a qualquer ponto da circunferência de raio 40   m m mostrada. Se θ = 20 ° , determinar: (a) a tensão em A .

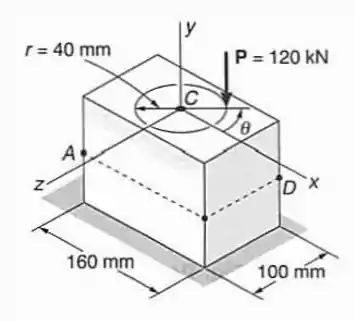
Passo 1

Para esse problema vamos calcular o momento que essa força P gera, os momentos de inércia I x e I z do corpo e as distâncias de forma que poderemos utilizar a expressão da tensão em função do momento:

σ A = - P A - M x ⋅ z A I x + M z ⋅ x A I z

Lembrando que o termo - P A é negativo porque se trata de uma força de compressão.

Passo 2

Então vamos calcular o momento que a força P gera:

M x = - P ⋅ R ⋅ s e n ⁡ ( 20 ° )

M x = - 120 ⋅ 0,040 ⋅ 0,342 = - 1,64   k N ⋅ m

M z = - P ⋅ R ⋅ c o s ⁡ ( 20 ° )

M z = - 120 ⋅ 0,040 ⋅ 0,934 = - 4,51   k N ⋅ m

Passo 3

Agora vamos calcular os momentos de inércia:

I x = 1 12 ⋅ 160 × 10 - 3 ⋅ ( 100 × 10 - 3 ) ³

I x = 1,333 × 10 - 5   m 4

I z = 1 12 ⋅ 1 0 0 × 10 - 3 ⋅ ( 1 6 0 × 10 - 3 ) ³

I z = 3,413 × 10 - 5   m 4

Passo 4

Agora as distâncias:

x A = - 160 2 = - 80   m m

z A = 100 2 = 50   m m

Passo 5

Finalmente podemos substituir na equação:

σ A = - P A - M x ⋅ z A I x + M z ⋅ x A I z

σ A = - 120000 ( 0,160 ⋅ 0,100 ) - - 1 64 0 ⋅ 0,050 1,333 × 10 - 5 + - 4 51 0 ⋅ - 0,080 3,413 × 10 - 5

σ A = - 7,5 + 6,15 + 10,57 = 9,22   M P a

Resposta

σ A = 9,22   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O anel aberto, com uma fenda, como mostrado, tem um raio interno r 1 = 20m m e seção circular com diâmetro d = 15m m . Sabendo-se que cada uma das forças 530N são aplicadas no centroide da seção trans
Considerando que o momento mostrado é substituído por uma força vertical de 10 kN aplicada no ponto D e no sentido descendente, determinar a tensão (a) ponto A; (b) ponto B
Três placas são soldadas juntas, para formar a viga curva mostrada. Para M = 1130N m , determinar a tensão no (a) ponto A; (b) ponto B; (c) centroide da seção transversal.
Um componente de máquina tem a seção transversal em forma de T , orientada como mostrado. Sabendo que M = 2500N ⋅ m , determinar a tensão no (a) ponto A (b) ponto B
Um componente de máquina tem a seção transversal em forma de T , orientada como mostrado. Sabendo que M = 2500N ⋅ m , determinar a tensão no (a) ponto A (b) ponto B