Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 124
Uma fresadora foi usada para remover uma porção de uma barra, ao longo de seu eixo. Sabendo-se que o diâmetro da barra é , e que forças de atuam nos centros das extremidades da barra, determinar:
- A tensão no ponto A.
- A tensão no ponto B.
- A posição da linha neutra da seção .
Passo 1
Nossos objetivos são dois, determinar a máxima tensão e a tensão no ponto F, sabemos que a fórmula da tensão é dada por:
Sabemos pelo enunciado que:
O momento precisamos da excentricidade, a excentricidade é a distância entre o ponto que definimos como o ponto que a carga age, até o ponto que sabemos que define a , como a nossa seção é , precisamos saber como determinar a linha neutra dela, e a fórmula é dada por:
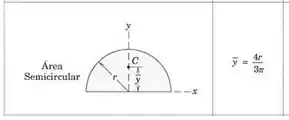
Olhando a nossa seção temos que:
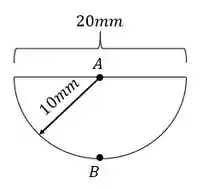
Calculando a LN, teremos que:
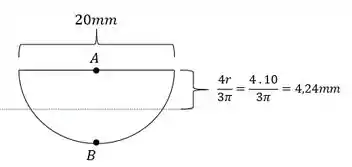
Que já nos dá exatamente a excentricidade da nossa carga, que podemos encontrar pela seguinte equação:
O momento de inércia e as áreas são:
Passo 2
Para o item A) queremos a máxima tensão que age na seção, para isso teremos que pegar o Y, sendo assim teremos que:
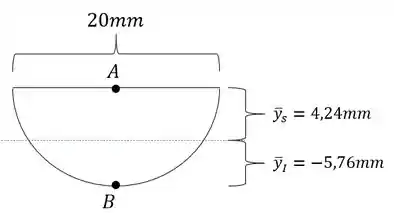
Como o momento fletor é negativo, precisamos do y positivo para termos a tensão em A, que nesse caso é de tração, sendo assim, termos que:
E para calcular a tensão no ponto B, precisamos do y negativo, dessa maneira, teremos que:
E para o item C, para determinarmos a LN na seção , precisamos lembrar que a seção tem tensão igual a zero exatamente sobre a LN, com isso podemos definir que:
Sabemos que:
Com isso teremos que:
Logo, se temos o valor de y, basta fazermos a diferença entre a LN anterior calculada e o valor de y definido, sendo assim teremos que:
Esse valor sendo visto de baixo pra cima, se olharmos de cima pra baixo teremos que:
Sendo assim a nova LN será definida da seguinte maneira:
