Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 171
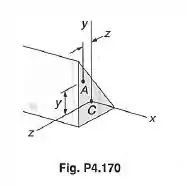
A viga do Prob. 4.170 está submetida a um momento atuando em um plano horizontal. Mostre que a tensão no ponto é:
Passo 1
Olha, aqui a gente vai ter que montar uma expressão para essa tensão causada pelo momento em e tentar chegar em:
Se a gente considerar que as tensões permanecem dentro do limite de proporcionalidade do material (regime elástico), dizemos que a tensão no ponto é proporcional a distância dele ao eixo e ao eixo .
Com isso, podemos escrever uma expressão genérica para :
Onde e são constantes. Aí a gente pode achar o valor dessas constantes para a situação do enunciado. Vem comigo!
Passo 2
Podemos lembrar que uma fórmulinha para o somatório de momentos em relação a é:
E se a gente substituir nossa expressão para a tensão:
Mas repara que essa primeira integral que apareceu é a definição de e a segunda é a definição de :
E agora a gente pode lembrar que no nosso problema, só há momento em . Então o momento em relação a é zero:
Passo 3
O somatório de momentos em relação a tem uma carinha parecida:
Substituindo nossa tensão:
De novo aparece as definições de na primeira integral e de na segunda:
Mas a gente tem uma expressãozinha para :
E voltando para achar :
Passo 4
Podemos voltar lá para nossa expressão e substituir as constantes:
Olha só! Era onde a gente queria chegar. Arrasamos!
Resposta
Prova nos passos