Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 46

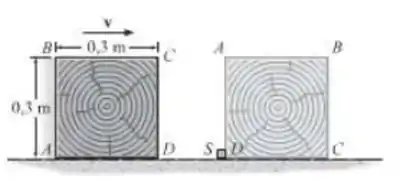
Um bloco de massa 5kg desliza sobre a superfície lisa quando o canto D bate em um bloco parado S. Determine a velocidade mínima “v” que o bloco deveria ter para que ele tombasse sobre seu lado e parasse na posição mostrada. Despreze a dimensão de S. Dica: Durante o impacto, considere o peso do bloco como não impulsivo.

Passo 1

Se o bloco se inclinar sobre o ponto D, ele deve pelo menos atingir a posição do traço mostrada. O ponto de referência é definido no ponto D.

Quando o bloco está na posição inicial e final, seu centro de gravidade está localizado 0,15 m e 0,21215 m acima do ponto de referência. Sua energia potencial inicial e final são (5)(9,81)(0,15) = 7,3575 J e (5)(9,81)(0,21215) = 10,406 J .O momento de inércia do bloco em torno do ponto D é:

I D = 1 12 5 0,3 2 + 0,3 2 + 5 0,15 2 + 0,15 2 = 0,3   K g . m ²

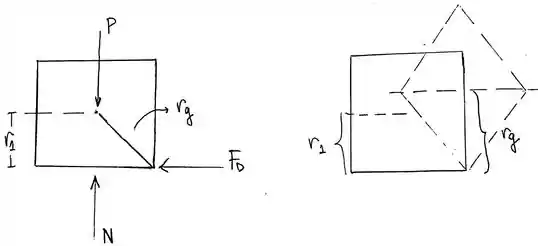
Passo 2

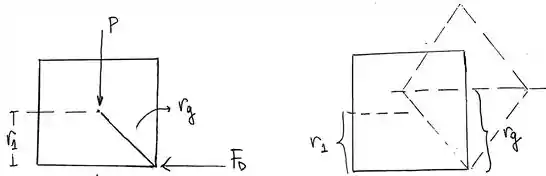
A energia cinética inicial do bloco (depois do impacto) é 1 2 I D W 2 2 = 1 2 ( 0,3 ) W 2 2 . Aplicando a equação de conservação da energia, temos:

T 2 + V 2 = T 3 + V 3

1 2 0,3 W 2 2 + 7,3575 = 0 + 10,406

W 2 = 4,5081   r a d / s

Resposta

Conservação do momento angular: Como o peso do bloco e a reação normal N são forças não impulsivas, o momento angular é conservado em torno do ponto D. Temos:

H D 1 = ( H D ) 2

m ( v g ) r 1 = I D W 2

5 v 0,15 = 0,3 4,5081

v = 1,8324   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os blocos A e B pesam 20 lb cada, o bloco C pesa 14 lb e o bloco D pesa 16 lb. Sabendo que uma força descendente de magnitude 24 lb é aplicada ao bloco D, determine (a) a aceleração de cada bloco, (b)
Uma esfera D de 100 g está em repouso em relação a um tambor que gira a uma taxa constante. Desprezando o atrito, determine o intervalo admissível da velocidade v da esfera se nenhuma das forças exerc
No Problema 12.63, determine o menor valor permitido da razão die em termos de e , m , v 0 e V se em x = l, a distância mínima permitida entre o caminho dos elétrons e a placa positiva é 0,05d.12.63 -
No tubo de raios catódicos mostrado, os elétrons emitidos pelo cátodo e atraídos pelo ânodo passam por um pequeno orifício no ânodo e viajam em linha reta com uma velocidade vo até atingirem a tela em
Uma série de pequenos pacotes, cada um com a massa de 0,5 kg, é descarregada de uma correia transportadora como mostrado na figura. Sabendo que o coeficiente de atrito estático entre cada pacote e a c