Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 93

O disco semicircular tendo uma massa de 10 kg está girando a ω = 4   r a d / s no instante θ = 60 ° . Se o coeficiente de atrito estático em A é μ s = 0,5 , determine se o disco desliza neste instante.

Passo 1

Começaremos o exercício calculando o momento de inércia do disco em relação ao seu centro de massa com o auxílio do diagrama a seguir:

I G = 1 2 m r 2 - m d 2 = 1 2 10 0,4 2 - 10 0,1698 2

I G = 0,5118   k g . m 2

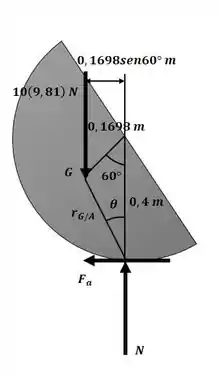
Ainda do esquema apresenta acima, podemos obter o valor de r G / A aplicando a lei dos cossenos:

r G / A 2 = 0,1698 2 + 0,4 2 - 2 0,1698 0,4 c o s 60 °

r G / A = 0,3477   m

E agora, usando a lei dos senos, podemos encontrar o valor de θ :

s e n θ 0,1698 = s e n 60 ° 0,3477 → θ = 25,01 °

Passo 2

Agora aplicando o somatório de momento com relação ao ponto A, ainda com o auxílio da figura do passo 1, temos:

↺ +   ∑ M A = ∑ M k A

10 9,81 0,1698 s e n 60 ° = 0,5118 α + 10 a G x c o s 25,01 ° 0,3477 + 10 a G y s e n 25,01 ° ( 0,3477 )

Essa será nossa equação 1. Agora iremos aplicar o somatório de forças na direção x ainda para a figura do passo 1:

+ ←   ∑ F x = m a G x

F a = 10 a G x

Essa será nossa equação 2. Agora aplicando o somatório de forças na direção y:

+ ↑   ∑ F y = m a G y

N - 10 9,81 = - 10 a G y

Essa será nossa equação 3.

Passo 3

Assumiremos que o disco não desliza em A para fazer a análise, então a A x = 0 . Sendo assim, aplicando a equação da aceleração do capítulo 16 para o diagrama a seguir:

a G = a A + α × r G / A - ω 2 r G / A

- a G x i - a G y j = 6,4 j + α k × - 0,147 i + 0,3151 j - 4 2 ( - 0,147 i + 0,3151 j )

- a G x i - a G y j = 2,3523 - 0,3151 α i + ( 1,3581 - 0,147 α ) j

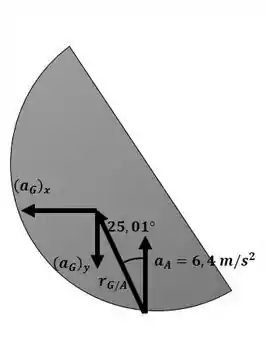
Igualando as componentes, nós temos:

a G x = 0,3151 α - 2,3523

a G y = 0,147 α - 1,3581

Essas serão nossas equações 4 e 5, respectivamente. Agora substituindo essas duas últimas equações na equação 1, temos:

10 9,81 0,1698 s e n 60 ° = 0,5118 α + 10 a G x c o s 25,01 ° 0,3477 + 10 a G y s e n 25,01 ° ( 0,3477 )

10 9,81 0,1698 s e n 60 ° = 0,5118 α + 10 ( 0,3151 α - 2,3523 ) c o s 25,01 ° 0,3477 + 10 ( 0,147 α - 1,3581 ) s e n 25,01 ° ( 0,3477 )

Resolvendo para α , temos:

α = 13,8   r a d / s 2

Substituindo esse valor nas equações 4 e 5:

a G x = 0,3151 13,8 - 2,3523 → a G x = 2,01   m / s 2

a G y = 0,147 13,8 - 1,3581 → a G y = 0,678   m / s 2

Agora substituindo esses valores nas equações 2 e 3:

F a = 10 2,01 → F a = 20,1   N

N - 10 9,81 = - 10 0,678 → N = 91,3   N

Como F a < F a m a x = μ s N = 0,5 91,3 = 45,66   N , então o disco não desliza.

Resposta

O disco não desliza

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o momento de inércia I y do sólido formado girando-se a área sombreada em torno do eixo y . A densidade do mateirla é ρ . Expresse o resultado em termos da massa m do semielipsoide.
Determine o momento de inércia I y do sólido formado girando-se a área sombreada em torno do eixo y . A densidade do mateirla é ρ . Expresse o resultado em termos da massa m do sólido.
O pêndulo consiste de uma placa tendo uma massa de 6kg e uma barra fina tendo uma massa de 2kg. Determine o raio de giração do pêndulo em relação a um eixo perpendicular à página e passando pelo ponto
O pêndulo consiste da barra fina de 3kg e a placa fina de 5kg. Determine a localização y - do centro de massa G do pêngulo; em seguida, calcule o momento de inércia do pêndulo em relação a um eixo per
Determine o momento de inércia da massa da placa fina em relação a um eixo perpendicular à página e passando pelo ponto O . O material tem uma massa por unidade de área de 20kg/m2.