Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 76
Um bloco de peso é colocado em contato com a superfície de uma viga, em um certo ponto , e então é largado. Mostrar que a máxima deflexão resultante em é duas vezes maior do que a deflexão devida a uma carga estática, aplicada em , de mesmo valor .
Passo 1
Fala, pessoal! Como anda a vida? Bora fazer um exercício de carga produzida por choque?
O enunciado quer que a gente compare a deformação sofrida por uma mesma viga em dois casos. No caso 1 a viga sofre o impacto de um bloco de peso que é largado a uma altura da viga. Esse impacto gera uma força na viga e gera uma deflexão no ponto da viga onde ocorre o impacto. Nesse caso, a energia potencial do bloco é absorvida pela viga.
No caso 2, uma força estática é aplicada no ponto da viga, causando uma deflexão nesse ponto . Essa deformação pode ser encontrada no apêndice do livro.
O enunciado quer que a gente mostre que:
A figura abaixo mostra esses dois casos.
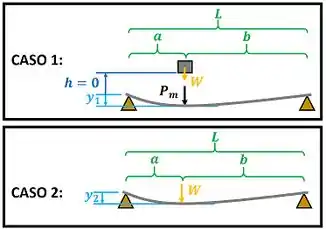
No próximo passo vamos começar as contas determinando o valor de .
Passo 2
é obtido na equação presente no apêndice .
onde é o módulo de elasticidade do material da vida e é o momento de inércia do perfil da viga.
Passo 3
Foi tranquilo achar , né? vai ser um pouquinho mais complicado!
Pra achar , temos que lembrar que existe uma equação para calcular em função da força produzida pelo impacto do bloco de massa .
Substituindo essa equação na outra equação de , obtemos.
A equação resultante mostra que só falta achar uma equação de em função de para conseguir comparar com .
Achamos essa equação no apêndice do livro.
Ao invés de substituir na equação de , vamos descobrir quanto vale primeiro.
Passo 4
Se a gente reorganizar a equação de , conseguimos descobrir quanto vale .
Substituindo essa equação na fórmula de , achamos:
Agora, vamos substituir na equação de que deduzimos no passo 3.
Lembrando que vale zero, encontramos:
Como a deflexão é maior que zero, podemos cortar ela dos dois lados da equação. Também podemos cortar !
Aeeeeee! Mostramos o que a questão queria!
Resposta
Ei, a resposta está no passo a passo :)