Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 75
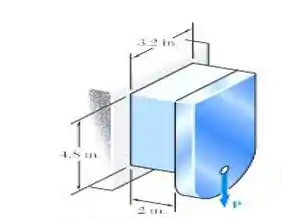
O bloco plástico mostrado na figura é colado a um suporte rígido e a uma placa vertical à qual é aplicada uma força P de 55kip. Sabendo que, para o plástico utilizado, determine o deslocamento da placa.
Passo 1
E aí gurizada tudo belezinha? O enunciado pede para que a gente determine o deslocamento da placa, para isso vamos esboçar um diagrama de corpo livre, vejam...
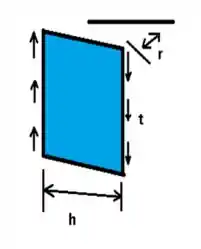
Agora devemos primeiramente determinar a área, lembrando que
Agora sim podemos determinar a tensao de cisalhamento
Sabendo que temos entao:
A espessura é dada por , assim o deslocamento é dado por:
Resposta
Exercícios de Livros Relacionados
A haste é feita de alumínio 2014 -T 6 . Se for submetida à carga de tração de 700N e tiver diâmetro de 20mm , determine as deformações principais em um ponto sobre a superfície da haste.
As deformações principais em um ponto sobre a superfície de alumínio de um tanque são ϵ 1 = 630 ( 10 - 6 ) e ϵ 2 = 350 ( 10 - 6 ) . Se for um caso de estado plano de tensão, determine as tensões princ
Uma carga periférica uniforme de 100kN/m e 70kN/m é aplicada a um corpo de prova de poliestireno. Se a forma original do corpo de prova for quadrada, de dimensões a = 50mm , b = 50mm e espessura t = 6
As tensões principais em um ponto são mostradas na figura. Se o material for grafite, para o qual E g = 5,6GPa e ν = 0,23 , determine as deformações principais.
Uma haste tem raio de 10mm . Se for submetida a uma carga axial de 15N tal que a deformação axial na haste seja ϵ x = 2,75 ⋅ 10 - 6 , determine o módulo de elasticidade E e a mudança em seu diâmetro.