O bloco de é rebocado para cima na rampa do carrinho de usando-se o motor montado ao lado do carrinho. Se o motor enrola o cabo a uma velocidade constante de , medida relativamente ao carrinho, determine a distância que o carrinho percorrerá quando o bloco tiver viajado uma distância , rampa acima. Tanto o bloco quanto o carrinho estão em repouso quando . O coeficiente de atrito cinético entre o bloco e a rampa é . Despreze a resistência ao rolamento.
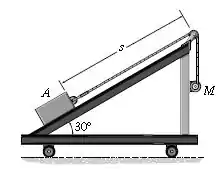
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Aplicando conservação de quantidade de movimento:
Substituindo os valores, temos:
Analisando o movimento relativo, temos:
Resolvendo o sistema, temos:
Passo 2
O tempo do movimento é dado por:
A distância percorrida pelo carro durante o tempo , é dada por: