Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 82

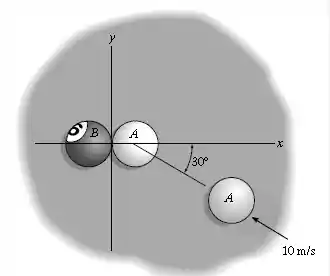
A bola de bilhar A move-se com uma velocidade de 10   m / s imediatamente antes de atingir a bola B , que está em repouso. Se as massas de A e B são 200   g cada e o coeficiente de restituição entre elas é e = 0,8 , determine a velocidade de ambas as bolas logo após o impacto.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos aplicar a conservação de quantidade de movimento linear paras as bolas A e B , para analisar as velociadades antes e após o impacto.

Como A tem componentes das velocidade em y e x , então vamos analisar para os dois eixos:

← +     ∑ m 1 v x 1 = ∑ m 2 v x 2

m A v A x + m B v B x = m A v A ' x + m B v B ' x

0,2 10 cos ⁡ 30 ° = 0,2 v A ' cos ⁡ θ A + 0,2 v B ' cos ⁡ θ B

v A ' cos ⁡ θ A + v B ' cos ⁡ θ B = 8,6603

Para o eixo y , temos?

m A v A x = m A v A ' x

0,2 10 sin ⁡ 30 ° = 0,2 v A ' sin ⁡ θ A

v A ' sin ⁡ θ A = 5

E:

m B v B x = m B v B ' x

0 = 0,2 v B ' sin ⁡ θ B

v B ' sin ⁡ θ B = 0

Fazendo uma analise rápida, é possível notar que desde que v B ' seja diferente de zero, teremos que   θ B é zero.

θ B = 0 °

Vamos aplicar o conceito de restituição ao sistema:

e = v B ' x - v A ' x v A x - v B x

0,8 = v B ' cos ⁡ θ B - v A ' cos ⁡ θ A 10 cos ⁡ 30 ° - 0

v A ' cos ⁡ θ A = v B ' cos ⁡ 0 ° - 8 cos ⁡ 30 °

v B ' - v A ' cos ⁡ θ A = 8 cos ⁡ 30 °

Podemos somar as equações:

v B ' - v A ' cos ⁡ θ A + v A ' cos ⁡ θ A + v B ' = 8 cos ⁡ 30 ° + 8,6603

2 v B ' = 15,6  

v B ' = 7,8   m / s

Logo:

Podemos dividir as seguintes equações:

v A ' sin ⁡ θ A v A ' cos ⁡ θ A = 5 v B ' - 8 cos ⁡ 30 °

tan ⁡ θ A = 5 7,8 - 6,93

θ A = tan - 1 ⁡ 5,75

θ A = 80,2 °

Portanto:

v A ' sin ⁡ 80,2 ° = 5

v A ' = 5,07   m / s

Resposta

θ B = 0 °

v B ' = 7,8   m / s

θ A = 80,2 °

v A ' = 5,07   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O superpetroleiro tem um deslocamento (massa) total de 150 ( 10 3 ) toneladas métricas (uma tonelada métrica é igual a 1000k g ) e está parado na água quando o rebocador começa a puxar. Se uma tração
O bloco de 10k g está se deslocando para a esquerda com uma velocidade de 1,2m / s no instante de tempo t = 0 , quando a força P é aplicada como mostrado no gráfico. A força continua no nível de 10N .
O sistema hidráulico dos freios para o caminhão e o reboque são regulados para produzir forças de frenagem iguais para as duas unidades. Se os freios são aplicados de maneira uniforme por 5 segundos p
O carro B ( 1500k g ) viajando para oeste a 48k m / h colide com o carro A ( 1600k g ) viajando para o norte 32k m / h conforme indicado. Se os dois carros ficam presos e se deslocam em conjunto como
O carro B está inicialmente parado e é atingido pelo carro A que se desloca com velocidade inicial v 1 = 30k m / h . Os carros ficam presos e se deslocam juntos com velocidade v ' após a colisão. Se o