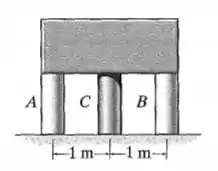
O bloco rígido pesa e será suportado pelos postes e , feitos de aço , e pelo poste , feito de latão vermelho . Se todos os postes tiverem o mesmo comprimento original antes de serem carregados, determine a tensão normal média desenvolvida em cada um deles, quando o poste for aquecido de modo que sua temperatura aumente . Cada poste tem área de seção transversal de .

Começamos com diagrama de corpo livre.

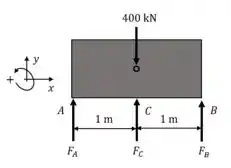
Vejamos no que a as condições de equilíbrios nos ajudam. Equilíbrio de momentos:

Equilíbrio de forças:

Temos duas incógnitas e uma equação. Precisamos de mais uma. Ela vai vir da geometria do problema e da deformação, vem ver!

Os postes e irão se deformar por causa do peso do bloco, reduzindo um comprimento .

O poste também vai reduzir por causa do bloco ( , mas vai estender por causa da mudança de temperatura (. O deslocamento total do ponto para baixo é

Ve que a temperatura causa um aumento do bloco, logo, para o nosso referencial (deslocamento para baixo), ele fica negativo.

O bloco é rígido (ele não vai se curvar), logo os dois postes da ponta precisam ter sempre o mesmo comprimento porque são iguais e sofrem a mesma carga.

Assim, já que temos simetria no problema, e nosso bloco não pode se curvar, tipo, ele não pode fazer algo assim:

Aí o poste do meio precisa também ter sempre o mesmo comprimento que os outros postes das pontas. Daí tiramos que todos os postes devem deformar o mesmo comprimento!

Essa é a nossa condição de compatibilidade. Temos fórmulas para calcular esses termos!

Para a mudança de temperatura, usamos a relação da dilatação térmica:

E para o efeito do peso, usamos a relação carga-deslocamento:

Opa, então a condição de compatibilidade vai usar força, que é o que procuramos.

Vamos dar uma ajeitada nas contas e aí resolvemos o sistema de equações.

Substituindo nossos dados

Agora substituímos em (equação do passo 1) para achar

Divida as forças pela área para acabar a questão:

Prontinho! Arrasamos!