Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 150

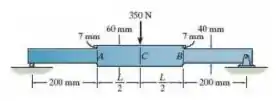
Determine o comprimento L da porção da barra de modo que as tensões de flexão máximas em A, B e C sejam as mesmas. A barra tem espessura de 10 mm.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 20 minutos?? Bora. Tá, o nosso enunciado nos pede o comprimento L para que os momentos internos nos pontos A, B e C sejam iguais. Nem parece tão difícil, é só a gente olhar para aquele ponto lá de cima e fazer. Partiu??

Passo 2

Nosso primeiro passo vai ser achar os momentos equivalentes para cada ponto; para isso, vamos montar nosso DCL e analisar tudo direitinho. Como a nossa força é aplicada exatamente no centro da barra e ela é dimensionada uniformemente, apenas com os dois apoios, sabemos que cada reação de apoio será igual à metade da força.

M a = 0,2   x   175 = 35   N . m

∑ M b = 0

M b - 0,2   x   175 = 0       ∴       M b = 35   N . m

∑ M c = 0

M c - 175   x   0,5 L + 0,2 = 0       ∴       M c = 87,5 L + 35

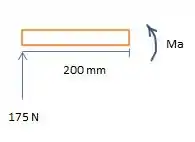
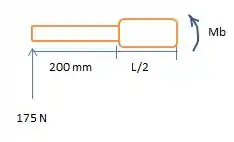
Como a barra é simétrica, ou seja, os dois lados têm estreitamentos iguais, as medidas para W ( W = 60   m m ) , r( r = 7   m m ) e h ( h = 40   m m ) serão as mesmas. Assim, quando fizermos as relações, teremos o nosso K.

r h = 0,175

W h = 1,5       ∴         K = 1,5

Passo 3

Pronto!! Agora vamos jogar tudo lá na nossa formulinha, calcular o nosso momento máximo em B e em C e igualar.

σ = K .   M c I  

σ b =   1,5   x   35   x   0,02 0,01   x   0,04 ³ 12     ∴   σ b = 19,6875     M P a

σ c =   ( 87,5   L + 35 ) ( 0,03 ) 0,01   x   0,06 ³ 12     ∴   σ c = 14,583 3 3   L + 5,8333 M P a

σ b =   σ c 19,6875 = 14,58333   L + 5,8333       ∴         L = 950   m m

Resposta

L = 950   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma viga com a seção transversal mostrada na figura é constituída de um aço elastoplástico, com E = 200 G P a e σ e = 240M P a . Para flexão em torno do eixo z, determine o momento fletor no qual.Inic
Resolva o P r o b . 4.71 assumindo que os momentos aplicados MeM ’ são orientados paralelamente ao eixo x .
Determine o momento de plastificação M p da viga de aço cuja seção transversal é a mostrada, assumindo que o aço é elastoplástico com resistência ao escoamento de 42ksi
Determine o momento plástico M p de uma viga de aço de seção transversal mostrada na figura. Considerando que o aço seja elastoplástico com uma tensão de escoamento de 240M p a .
Determine o momento plástico M p de uma viga de aço de seção transversal mostrada na figura. Considerando que o aço seja elastoplástico com uma tensão de escoamento de 240M p a .