Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 48
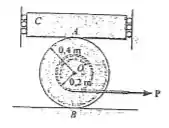
O bloco tem uma massa de e está confinado entre duas paredes por roletes lisos. Se o bloco se apoia no topo do carretel de determine os coeficientes de atrito estático exigidos em e de modo que o carretel deslize em e quando a intensidade da força aplicada for aumentada para .
Passo 1
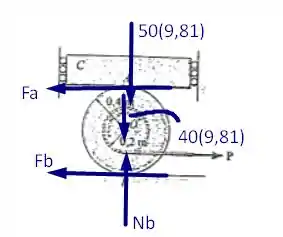
Desejamos encontrar os valores dos coeficientes de atrito dadas as condições especificadas no enunciado e valor de dado que é . Tomemos, então, o seguinte diagrama de forças
Passo 2
Substituindo o valor de em vamos encontrar
Temos que a força de atrito é dada por . Dessa forma para o caso de vamos ter
Resposta
Exercícios de Livros Relacionados
A bobina com massa de 150k g se apoia sobre o piso em A e contra a parede em B. Determine as forças que agem na bobina em A e B se P=800N . O coeficiente de atrito estático entre a bobina e o piso no
O freio manual consiste em uma alavanca conectada por um pino e um bloco de atrito em B. O coeficiente de atrito estático entre a roda e a alavanca é u=0,3 , e um torque de 5Nm é aplicado à roda. Dete
O carro tem massa de 1,6M g e centro de massa em G. Se o coeficiente de atrito estático entre o acostamento da estrada e os pneus é u=0,4 , determine a maior inclinação θ que o acostamento pode ter se
O anel tem massa de 0,5k g e está apoiado sobre a superfície da mesa. Em um esforço para mover o anel, o dedo exerce uma força P sobre ele. Se essa força for direcionada para o centro O do anel, confo
O freio manual é usado para interromper o giro da roda quando ela está sujeita a um momento de binário M 0 . Se o coeficiente de atrito estático entre a roda e o bloco é u , determine a menor força P