Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas fundamentais - Ex. 5
Determine a força mínima que pode ser aplicada sem causar o movimento da caixa de com centro de gravidade em . O coeficiente de atrito estático no piso é .
Passo 1
Desejamos encontrar o valor mínimo de que pode ser aplicado sem causar o movimento da caixa de . Tomemos, então, o seguinte diagrama de corpo livre
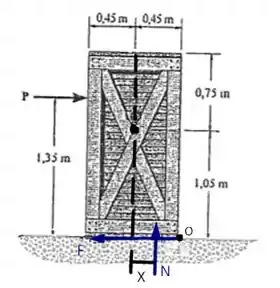
Como nesse caso não temos um plano inclinado podemos inferir que a normal vai ser igual ao peso da caixa dado por .
Analisando, agora, as forças que atuam no eixo podemos fazer o seguinte
Passo 2
Agora, quando a caixa estiver na iminência de se mover, ou seja, a força for igual a nós teremos
Analisando, agora, o momento vamos ter
Como o nosso ponto está depois do nosso ponto vemos que se aumentarmos mais um pouquinho a geladeira vai tombar. Sendo assim, pode variar até um valor de (prezando pela certeza de não ocorrer nenhum incidente) sem risco de tombamento.