Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 121
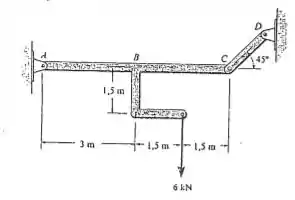
Determine o esforço cortante e o momento fletor interno no membro como uma função de , onde a origem para está em .
Passo 1
Desejamos calcular o valor dos esforços internos no membro como sendo função de e a origem sendo . Dessa forma, tomemos os seguintes diagramas de forças
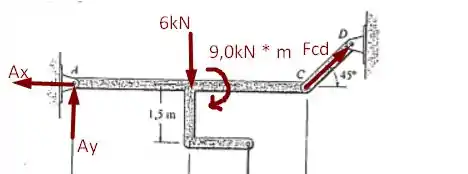
Para calcular os esforços internos, podemos dividir o segmento em duas partes onde teremos
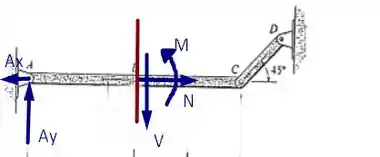
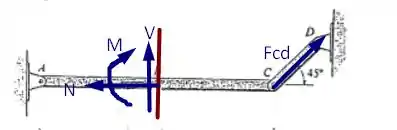
Passo 2
De podemos equacionar o seguinte
Passo 3
Para o esforço cortante e momento fletor devemos avaliar até metade da barra e da metade até a outra extremidade. Dessa forma, para temos
Para a outra metade da nossa barra vamos ter
Resposta
Exercícios de Livros Relacionados
Determine as forças normal e cortante e o momento fletor nos pontos E e F da viga.
Determine as forças normal e cortante e o momento fletor no ponto C da viga.
Determine as forças normal e cortante e o momento fletor no ponto C .
Determine as forças normal e cortante e o momento fletor nos pontos E e F da viga composta por três elementos. O ponto E está localizado logo à esquerda da força de 800N .
Determine as forças normal e cortante e o momento fletor nos pontos D e E da viga com o trecho D C em balanço. O ponto D está localizado logo à esquerda do suporte de rolete em B , onde o momento de b