Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 5

Se os blocos A e B de massa 10 kg e 6 kg, respectivamente, são colocados sobre o plano inclinadoe soltos, determine a força desenvolvida na barra de conexão. Os coeficientes de atrito cinético entre os blocos e o plano inclinado são μ A = 0,1     e   μ B   = 0,3 . Despreze a massa da barra de conexão.

Passo 1

O primeiro passo para determinar a força desenvolvida F na barra, é obter a equação do movimento do bloco A e do bloco B . Do diagrama de corpo livre, temos:

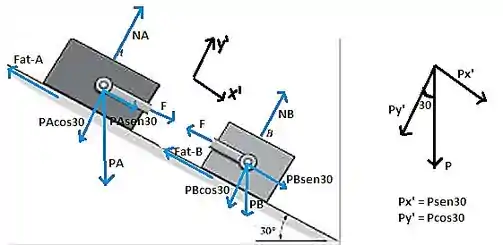
Diagrama de corpo livre do bloco A :

∑ F y ' = m A a y '

N A - P A cos ⁡ 30 =   m A a y '

Como não há movimento na direção y ’ , concluímos que:

N A - P A cos ⁡ 30 = 0

N A =   P A cos ⁡ 30 = m A g c o s 30

N A = 10 × 9,81 c o s 30 = 84,96 N

∑ F x ' = m A a x '

F + P A sin ⁡ 30 - f a t A = m A a x '

Por definição a força de atrito é igual a:

f a t =   μ N

Então:

F + m A g . sin ⁡ 30 - μ A N A = m A a x '

F + ( 10 × 9,81 ) sin ⁡ 30 - 0,1 × 84,96 = 10 a x '

44,55 + F = 10 a x '

Diagrama de corpo livre do bloco B :

∑ F y ' = m   B   a y '

N B - P B cos ⁡ 30 =   m A a y '

Como não há movimento na direção y ’ , concluímos que:

N B - P B cos ⁡ 30 = 0

N B =   P B cos ⁡ 30 = m B g c o s 30

N B = 6 × 9,81 c o s 30 = 50,97 N

∑ F x ' = m B a x '

P B sin ⁡ 30 - F - f a t B = m B a x '

m B g . sin ⁡ 30 - F - μ B N B = m B a x '

( 6 × 9,81 ) sin ⁡ 30 - F - 0,3 × 50,97 = 6 a x '

14,14 - F = 6 a x '

Passo 2

Agora que obtemos duas equações e temos duas incógnitas a solucionar, podemos determinar a aceleração a x ' e a força F da seguinte maneira:

44,55 + F = 10 a x ' +

14,14 - F = 6 a x '

44,55 + 14,14 = ( 10 + 6 ) a x '  

a x ' = ( 44,55 + 14,14 ) ( 10 + 6 ) = 3,42   m / s 2

Substituindo o valor encontrado da aceleração em uma das equações acima, encontraremos o valor de F :

F =     14,14 - 6 × 3,42 = - 6,37 N

Resposta

A força desenvolvida na barra de conexão é igual a 6,37 N.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O ar é movimentado através do duto estacionário A com uma velocidade de 15m / s e descarregado através de uma seção B C de um bocal experimental. A pressão estática manométrica média através da seção
O helicóptero mostrado tem uma massa m e paira nessa posição transmitindo uma quantidade de movimento descendente para uma coluna de ar definida pela fronteira indicada do turbilhão da hélice. Encontr
A válvula, que está aparafusada na tubulação fixa na seção A A , é projetada para descarregar água doce à taxa de 1,30m 3 / m i n para o ambiente no plano x y como mostrado. A pressão da água em A A é
Um jato de ar em alta velocidade escoa do bocal A com 40m m de diâmetro a uma velocidade v de 240m / s e atinge a pá O B , mostrada em sua vista lateral. A pá e sua extensão em ângulo reto têm massas
Um corte axial do bocal de sucção A para um descarregador de trigo a granel é mostrado aqui. O tubo externo é preso ao tubo interno por várias nervuras longitudinais que não limitam o escoamento do ar