Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 46
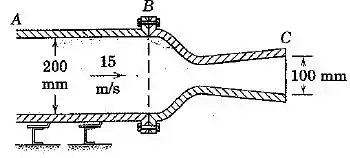
O ar é movimentado através do duto estacionário com uma velocidade de e descarregado através de uma seção de um bocal experimental. A pressão estática manométrica média através da seção é , e a massa específica do ar a essa pressão e na temperatura característica é de . A pressão estática manométrica média através da estação de saída é medida ser , e a massa específica correspondente do ar é de . Calcule a força exercida sobre o flange do bocal em pelos parafusos e a vedação para segurar o bocal no lugar.
Passo 1
Já que o duto é estacionário, nós sabemos que a taxa de escoamento de massa é igual em qualquer ponto do sistema:
Vamos lembrar da equação para essa taxa:
E já temos todas as variáveis dessa equação, exceto . Calculando as áreas e a partir dos diâmetos, ficamos com as seguintes expressões:
E então:
Passo 2
Beleza, mas nosso objetivo é calcular a força realizada em . Vamos escrever a equação para a força em um duto de escoamento:
Nesse caso, além da força realizada em , temos as duas pressões e agindo em sentidos opostos uma à outras (não esqueça de multiplicar as pressões pelas respectivas áreas!):
A força atua no mesmo sentido da pressão , porque ela existe justamente para resistir ao efeito da pressão , que pressiona as paredes para fora. Então:
Passo 3
Agora já temos todos os valores para substituir! Só falta calcular a taxa usando qualquer uma das duas expressões do passo :
Agora é só substituir:
Resposta
A força é .