Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 45
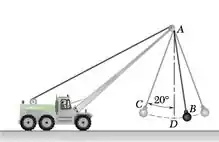
Uma bola de demolição B de 60 kg está presa a um cabo de aço AB de 15 m de comprimento e oscila no arco vertical mostrado na figura. Determine a tração no cabo (a) no ponto mais alto C da oscilação, (b) no ponto mais baixo D da oscilação, onde a velocidade escalar de B é de 4,2 m/s.
Passo 1
O enunciado pede que a gente determine no ponto mais alto C da oscilação, no ponto mais baixo D da oscilação, onde a velocidade escalar de B é de 4,2 m/s, então partiu :D
- Em C, o topo do balanço, vb = 0; portanto
ou
Passo 2
ou
Resposta
Exercícios de Livros Relacionados
As três barras idênticas, cada uma com massa de 8k g , são unidas pelos dois conectores livremente articulados de massa desprezível e estão em repouso sobre uma superfície horizontal lisa. Calcule a a
Calcule a aceleração do centro de massa do sistema de quatro cilindro de 10k g . Despreze o atrito e a massa das polias e cabos.
As duas esferas de 2k g estão inicialmente em repouso sobre a superfície horizontal quando uma força vertical F = 60N é aplicada à junção dos fios aos quais estão conectadas como mostrado. Calcule a c
Para o sistema de partículas do Prob. 4/1, determine H G e H ˙ G .
Os vagões de mina com 300k g e 400k g estão se movendo em sentidos opostos ao longo do trilho horizontal com as respectivas velocidade de 0,6m / s e 0,3m / s . Após o impacto os vagões se tornam acopl