Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 43

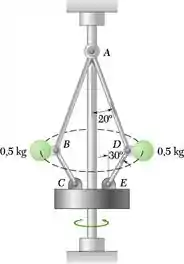
As esferas de 0,5 kg de um regulador centrífugo giram a uma velocidade escalar constante v no círculo horizontal de 0,15 m de raio, tal como mostra a figura. Desprezando a massa das hastes AB, BC, AD e DE e exigindo que as hastes suportem somente forças de tração, determine o intervalo de valores admissíveis de v de modo que as intensidades das forças nas hastes não ultrapassem 75 N.

Passo 1

O enunciado pede que a gente determine o intervalo de valores admissíveis de v de modo que as intensidades das forças nas hastes não ultrapassem 75 N.

Temos que a aceleração é dada por:

a = a n = v 2 ρ

onde

ρ = 0,15   m

← + Σ F x = m a :         T D A sin ⁡ 20 ° + T D E sin ⁡ 30 ° = W g v 2 ρ

+ ↑ Σ F y = 0 :       T D A cos ⁡ 20 ° - T D E cos ⁡ 30 ° - W = 0

Observe que a Eq. (2) implica que

  1. quando

    2. T D E = ( T D E ) max ,         T D A = ( T D A ) max

T D E = ( T D E ) min ,         T D A = ( T D A ) min

Passo 2

Caso 1: TDA é máximo.

Seja

T D A = 75   N

Eq (2)

75 cos ⁡ 20 ° - T D E cos ⁡ 30 ° - 0,5 = 0

ou

T D E = 162,75   N     inaceitável  > 75   N

Agora deixe

T D E = 75   N

T D A cos ⁡ 20 ° - ( 75 ) cos ⁡ 30 ° - 0,5 = 0

ou

T D A = 69,65         O.K.         ( < 75   N )

( T D A ) max = 69,65   N

( T D E ) max = 75   N

Passo 3

Eq. (1)

( v 2 ) ( T D A ) max = 9,81 0 . 15 0,5 69,65 sin ⁡ 20 ° + 75 sin ⁡ 30 °   N

ou

v ( T D A ) max = 13.85   m/s

Agora nós formamos

cos ⁡ 30 ° 1 + sin ⁡ 30 ° 2

T D A sin ⁡ 20 ° cos ⁡ 30 ° + T D A cos ⁡ 20 ° sin ⁡ 30 ° = W g v 2 ρ cos ⁡ 30 ° + W sin ⁡ 30 °

ou

T D A sin ⁡ 50 ° = W g v 2 ρ cos ⁡ 30 ° + W sin ⁡ 30 °

v max   ocorre quando   T D A = ( T D A ) max

v max = 13.85   m /s

Passo 4

Caso 2: TDA é mínimo.

Porque ( T D A ) min   ocorre quando T D E = ( T D E ) min ,

seja T D E = 0 .

Eq. (2)

T D A cos ⁡ 20 ° - 0,5 = 0

ou

T D A = 0,43 < 75     O.K.

Nota: Eq. (3) implica que quando T D A = ( T D A ) min ,   v = v min . Então

Eq. (1)

( v 2 ) min = 9,81 0 . 15 1,5 0,43 sin ⁡ 20 °

ou

( v C ) min = 0,37   m / s

0 ≤ T A B ,   T B C , T A C , T D E ≤ 75   N

Resposta

0,37 m s ≤ v ≤ 13,85 m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois projéteis, cada um com massa de 10k g , são disparados simultaneamente a partir do veículo de 1t mostrado, que está se deslocando com uma velocidade inicial v 1 = 1,2m / s no sentido oposto aos d
As duas pequenas esferas, cada uma com massa m , estão rigidamente conectadas por uma haste de massa desprezível. O centro C da haste possui uma velocidade v na direção x , e a haste está girando no s
Três macacos A , B e C , com massas de 10 , 15 e 8k g , respectivamente, estão subindo e descendo a corda suspensa a partir de D . No instante representado, A está descendo a corda com uma aceleração
O sistema de três partículas possui as massas, velocidades e forças externas indicadas nas partículas. Determine r - , r - ˙ , r - ¨ , T , H O e H O ˙ para esse sistema.
Os três vagões de carga estão se deslocando ao longo do trilho horizontal com as velocidades indicadas. Após os impactos ocorrerem, os três vagões se tornam acoplados e se movem com uma velocidade com