Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 95
O cabo de latão tem seção transversal triangular de em um lado. Se a tensão de escoamento para o latão for , determine o torque máximo ao qual o cabo pode ser submetido de modo a não sofrer escoamento. Se esse torque for aplicado a um segmento de de comprimento, determine o maior ângulo de torção de uma extremidade do cabo em relação à outra extremidade que não causará dano permanente ao cabo.
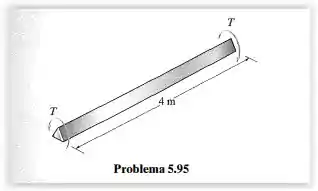
Passo 1
Olá pessoal, tudo bem?
Vamos lá! Essa questão nos pede duas coisas: o torque máximo que pode ser aplicado sem que o cabo sofra escoamento e o maior ângulo de torção de uma extremidade do cabo em relação à outra que não causará nenhum dano permanente a ele, sendo que o seu comprimento é .
Dados fornecidos:
Passo 2
Primeiro temos que descobrir qual o torque máximo admissível para que o material não sofra escoamento, ou seja, o torque que provocará uma tensão de .
Manipulando a equação para achar o torque temos:
Passo 3
Agora que já encontramos o valor do torque máximo, determinaremos o valor do ângulo provocado por essa torção de uma extremidade em relação a outra ().