Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 131
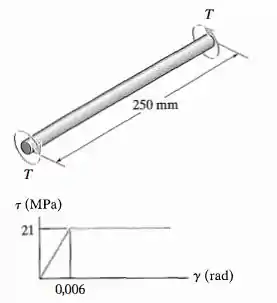
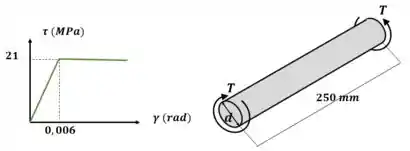
Um eixo de 37,5 mm de diâmetro é feito de um material elástico-plástico como mostra a figura. Determine o raio de seu núcleo elástico se ele for submetido a um torque de T=300 Nm. Se o eixo tiver 250 mm de comprimento, determine o ângulo de torção.
Passo 1
OBS: Há um erro nesta questão. Utilizando o diâmetro de encontramos um raio do núcleo elástico negativo. Isso indicaria que a torção tem característica totalmente plástica e não existiria núcleo elástico. Isso contradiz o próprio enunciado que afirma que o “diâmetro é feito de um material elástico-plástico”. Além disso, com as informações dadas na questão, não seria possível calcular o ângulo de torção. PARA A RESOLUÇÃO DA QUESTÃO SERÁ USADO O VALOR DE DIÂMETRO
Dados da questão:
A questão pede:
- O raio elástico-plástico
- O ângulo de torção
Estratégia de resolução:
- Como a questão já afirma que a torção é elástico-plástica, basta aplicar a equação 5.26 para determinar o raio elástico
- No ponto do raio elástico, sabemos que a deformação e a tensão são iguais a de escoamento. Com isso podemos olhar o gráfico e calcular o ângulo de torção
Passo 2
Para encontrar o raio elástico basta aplicar a equação 5.26
Isolando o raio elástico:
Substituindo o raio pelo diâmetro:
Substituindo os valores:
Passo 3
Para calcular o ângulo de torção usamos a equação 5.25
Substituindo os valores: