Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 72
O cabo e as polias são usadas para suspender a pedra de 300 kg. Determine a força que precisa ser exercida no cabo em A e a intensidade correspondente da força resultante que a polia C exerce no pino B quando os cabos estão na posição mostrada.
Passo 1
O primeiro passo é relembrar que para um mesmo fio/cabo, a tração é a mesma. Então é interessante começar desenhando o diagrama do corpo livre (DLC) das polias de interesse para entender a questão:
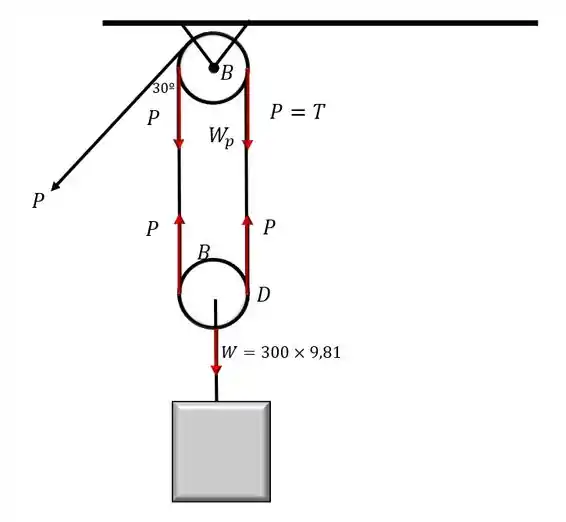
Passo 2
Com o diagrama do corpo livre pronto, podem-se escrever as equações do equilíbrio para as corpos no eixos x e y:
Polia de pino D:
Sendo
Para o pino B:
- No eixo x:
- No eixo y:
Passo 3
Enfim, pode-se calcular a força resultante no pino B:
Resposta
Exercícios de Livros Relacionados
Desenhe o diagrama de Corpo Livre da treliça que é sustentada pelo cabo AB e pelo pino C. Explique o significado de cada força no Diagrama
Determine as reações normais em A e B do Exercicio 1
Desenhe o diagrama de Corpo Livre da caçamba D do caminhão, que possui um peso de 25 kN e um centro de gravidade em G. Ela esta apoiada emum pino em A e um cilindro hidráulico conectado por pino em BC
Desenhe o diagrama de Corpo Livre da lança do guindaste AB, que possui peso 3,25 kN e um centro de gravidade em G. O apoio é sustentado por um pino em A em um cabo em BC. A carga de 6,25 kN é suspensa
Determine as componentes horizontais e verticais da reação no pino A e a tração desenvolvida no cabo BC usado para sustentar a estrutura de aço