Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 74
Determine as componentes horizontal e vertical da reação nos pinos A e C.
Passo 1
Começamos desenhando o diagrama do corpo livre da viga AB:
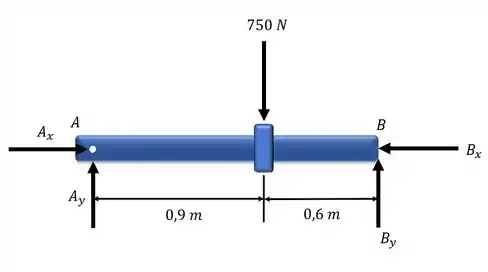
Aplicando a equação do equilíbrio para o momento no ponto A. A força de 750 N exerce momento no sentido horário e a força By exerce momento no sentido horário:
Passo 2
Aplicando a equação do equilíbrio no eixo y:
Substituindo a equação em :
Passo 3
Aplicando a equação do equilíbrio no eixo x:
Passo 4
Agora podemos desenhar o diagrama do corpo livre para o elemento BC:
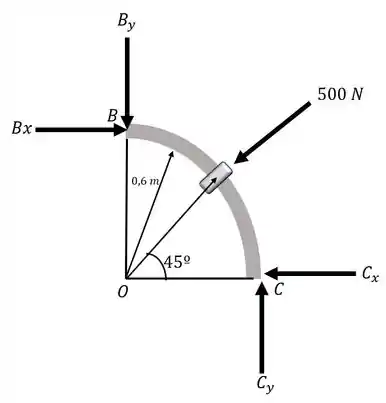
Aplicando a equação do equilíbrio no eixo y:
Substituindo em (:
Passo 5
Agora podemos utilizar a equação do equilíbrio para os momentos com relação ao ponto O (lembrando que podemos aplicar equações do momento para qualquer ponto, mesmo que estejam fora do corpo). A força Bx causa momento no sentido horário e Cy no sentido anti-horário.
Passo 6
Finalmente com o valor de Bx é possível achar o valor de Ax na equação :
Passo 7
Para achar o valor da componente Cx, podemos aplicar a equação do equilíbrio no corpo no eixo x:
Aplicando a equação em :