Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 98
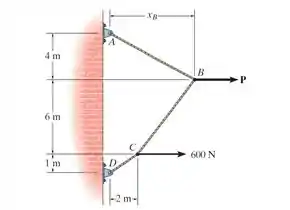
O cabo suporta a carga mostrada. Determine a intensidade da força horizontal de modo que .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Temos aqui nesta questão um cabo submetido a duas cargas concentradas, uma de e outra . Queremos descobrir qual é este valor de para que a distância seja iguala 5 m.
Para que calculemos este valor, será fundamental descobrirmos qual a força na corda , para que assim a gente consiga utilizar o método dos nós para o nó . Ou melhor se dizendo, que a gente relacione a força com a força .
Sendo assim, vamos fazer um corte na região e analisar as forças na parte .
Passo 2
Agora que a gente já sabe o que fazer, vamos as contas então!
Esboçando o diagrama de corpo livre, teremos:
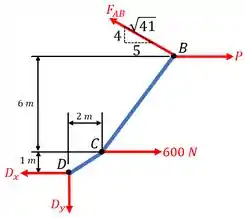
Apesar de não conhecermos a força na corda , sabemos que ela tem a mesma direção que a corda (por isto indicamos a direção pela relação do triângulo de catetos 4 e ).
Como o nosso objetivo aqui é relacionar a força com a força , basta fazermos o somatório de momentos em torno do ponto . Logo,
E assim conseguimos uma equação com duas incógnitas. Para que a gente consiga resolver a equação acima, precisamos de outra equação que relacione e para montar um sistema e resolvê-lo.
Passo 3
Para finalizarmos a questão, precisamos de outra equação que relacione e . Esta equação será obtida ao fazermos uma análise de equilíbrio no nó . Então, esboçando o diagrama de corpo livre neste ponto, temos:
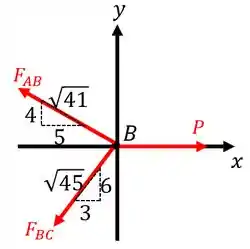
Como vocês podem ver do diagrama, acabou aparecendo mais uma incógnita . Entretanto, mesmo que a gente analise o equilíbrio em torno deste ponto, esta força não irá impedir que a gente obtenha o valor de .
Na verdade, a única influência será em dificultar um pouco mais as contas.
Bom, então vamos direto para elas! Aplicando as equações de equilíbrio, temos:
Da segunda equação obtemos que:
Substituindo na primeira iremos obter:
E por fim, se substituirmos na equação obtida no Passo 2, teremos:
E assim finalizamos a questão!