Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 76
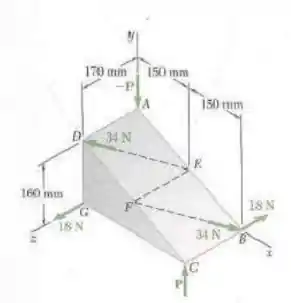
Sabendo que P=0, substitua os dois binários restantes por um binário único equivalente, especificando sua intensidade e a direção do seu eixo.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que tem essa rampa com esses dois momentos aplicados, mas nos pede para aplicar só um que dê o mesmo resultado e seu eixo de aplicação. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser achar o momento resultante.
Passo 3
Pronto!! Agora vamos achar o eixo de aplicação.
Resposta
Exercícios de Livros Relacionados
Determine os diagramas de esforço cortante e de momento fletor para a viga simplesmente apoiada.
Determine os diagramas de esforço cortante e de momento fletor para a viga.
Determine a força normal, a força cortante e o momento fletor na barra curva como uma função de θ .
A viga composta tem apoio fixo A , vinculação com pino em B e é suportada por um rolete em C . Determine os diagramas de esforço cortante e momento fletor para a viga.
Expresse as componentes internas de esfroço cortante e o momento fletor que atua na barra como uma função de y , onde 0 ≤ y ≤ 1,2m .