Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 70
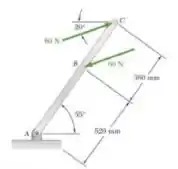
Duas forças paralelas de 60 N são aplicadas a uma alavanca como mostrado na figura. Determine o momento binário formado pelas duas forças (a) resolvendo para cada componente horizontal e vertical e adicionando os momentos dos dois binários resultantes, (b) usando a distância perpendicular entre as duas forças e (c) somando os momentos das duas forças com relação ao ponto A.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos diz que tem essa barra tem essas duas forças sendo aplicadas nela com aquelas inclinações ali e nos pede quanto vale seu momento binário. Partiu??
Passo 2
Ok, para o item a, nosso primeiro passo vai ser decompor as forças de B e C nos eixos horizontal e vertical. Para ficar mais fácil de calcular o nosso momento resultante, ou seja, da força C.
Agora que temos esses valores calculados, as distâncias entre as forças, em x e em y:
Pronto!! Agora vamos jogar tudo lá na nossa formulinha e teremos o nosso momento.
Passo 3
O angulo entre a direção das forças e a direção AC é de 35°. Logo, a distância perpendicular entre as forças é:
O momento binário é negativo pela regra da mão direita e dado por:
Passo 4
No item c, precisamos calcular a o momento de cada força separadamente, com relação ao ponto A, e somar. Logo, vamos calcular as distâncias perpendiculares do ponto A até a direção de cada força. A mais distante é:
A força de 60 N mais próxima, está a uma distância perpendicular do ponto A igual a:
Então momento ao redor do ponto A é:
Como é esperado, as 3 formas de calcular dão o mesmo resultado.