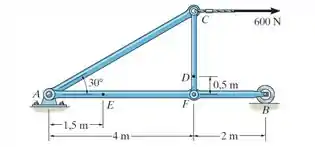
Determine a força normal, a força cortante e o momento fletor nos pontos e .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar a forças norma, cortante e o momento fletor nos pontos e , teremos que trabalhar com as barras e , respectivamente.
Entretanto, independente de quem a gente escolha para trabalhar primeiramente, vamos ter que determinar as reações em e na barra . Então, vamos começar a questão substituindo os vínculos por forças e esboçar o diagrama de corpo livre do sistema. Portanto,

Resolvendo o sistema acima obtemos e
Agora que a gente sabe as reações dos vínculos, vamos calcular o que a questão nos pede!
Passo 2
Vamos começar a determinar o que a questão nos pede pelo ponto . Só que para isto, precisamos da força na barra .
Então, vamos determinar quem é esta força. Analisando a barra , temos o seguinte diagrama de equilíbrio:
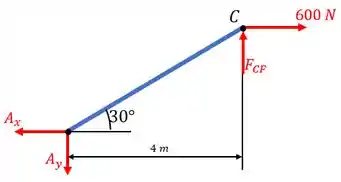
Fazendo o somatório de momentos em torno de , teremos:
Agora sim já podemos analisar a barra em si. Fazendo um corte no ponto , teremos:

Utilizando as equações de equilíbrio obtemos que , e , e assim finalizamos a primeira parte da questão!
Passo 3
Para finalizarmos a questão, basta analisarmos a barra . Fazendo um corte no ponto , teremos o seguinte diagrama de corpo livre:
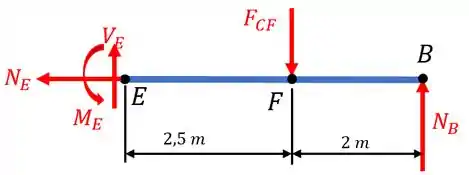
Utilizando as equações de equilíbrio obtemos:
Sistema cuja resposta é , e , e assim finalizamos a questão!