Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 116
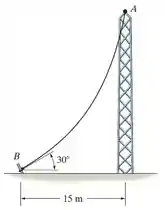
O cabo tem uma massa de e possui 25 m de extensão. Determine as componentes vertical e horizontal da força que ele exerce no topo da torre.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Queremos determinar as componentes vertical e horizontal da força que ele exerce no topo da torre sendo que o cabo está sujeito ao próprio peso de .
Bom, para que a gente possa determinar ambas as incógnitas, precisamos determinar as relações da equação da curva que define o cabo. E para isto, como o cabo está sujeito ao próprio peso, temos que começar resolvendo a seguinte integral:
Para nossa alegria, já sabemos que o resultado da integração acima é:
Passo 2
Agora temos que descobrir quem as constantes da nossa equação. Para isto, teremos que aplicar as condições de contorno do problema.
Fixando o sistema de coordenadas no ponto , teremos as seguintes condições: em , em e . Só que possamos aplicar estas condições, temos que manipular as nossas relações
Vamos começar aplicando . Para isto, precisamos lembrar que:
Sendo esse o mesmo da equação que obtivemos no Passo 1. Então, aplicando a condição, temos:
Aplicando a condição que quando , temos:
E por fim, para que a gente possa aplicar a condição em . Esta condição vem do fato do cabo ter 25 m de extensão. Então, aplicando-o, temos:
Resolvendo iterativamente esta equação nós obtemos que .
Passo 3
Agora já podemos partir para o cálculo da componente vertical no ponto , pois a horizontal nós já obtivemos, e é exatamente .
Já para a força vertical, vamos precisar da inclinação do cabo no ponto . Então, precisamos calcular o valor de quando .
Então, utilizando a relação desenvolvida no Passo 2, temos:
E a componente vertical será:
E assim finalizamos a questão!