Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 7.Problemas fundamentais - Ex. 11
Determine o esforço cortante e o momento fletor como uma função de , onde e , e depois contrua os diagramas de esforço cortante e de momento.
Passo 1
O problema quer que a gente calcule o esforço cortante e o momento fletor e um diagrama de esforço cortante.
Vamos começar notando que o momento momento encontra-se na metade da distância , então as forças em e , são iguais, vamos calcular o momento tendo como eixo de rotação:
E como são iguais , logo:
Vamos generalizar chamando de .
Passo 2
Então, vamos pegar o somatório das forças no eixo , e como a viga está em equilíbrio o somatório é , logo:
Passo 3
Agora, vamos calcular os momentos fletores em nas regiões onde pode adquirir valores, começaremos pela região :
Então vamos para o momento fletor na região :
Passo 4
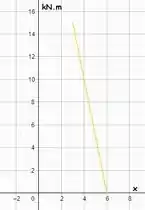
E no fim vamos fazer os diagramas de esforço, que ficam:
Na região .
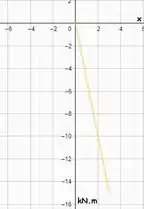
E na região :
