Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 110

Se o tubo tem uma massa por unidade de comprimento de 1500 kg/m, determine a tração mínima desenvolvida no cabo.

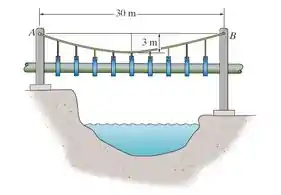
Passo 1

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

Queremos determinar a mínima tração desenvolvida no cabo.

Para que a gente possa determinar esta incógnita, precisamos determinar a equação da curva que define o cabo. E para isto, temos que resolver a seguinte integral:

y = 1 F H ∫ ∫ w x d x d x

Sendo w x o carregamento aplicado na corda. Nesta questão, a corda está submetida a um carregamento uniforme dado por:

w x = 1500 ⋅ 9,81 = 14715   N / m

Portanto, a nossa equação será:

y = 1 F H ∫ ∫ 14715 d x d x

y = 1 F H ∫ 14715 x + C 1 d x

y = 1 F H 7357,5 x 2 + C 1 x + C 2

Passo 2

Agora que obtivemos a equação da curvatura da corda, devemos aplicar as condições de contorno para descobrir as incógnitas C 1 , C 2 e F H .

Vamos fixar o sistema de coordenadas no ponto mais baixo do cabo, que está exatamente no meio do cabo. Aqui, temos as seguintes condições de contorno: y 0 = 0 , d y d x x = 0 = 0 e y 15 = 3 . Aplicando a primeira, temos:

y 0 = 1 F H 7357,5 ⋅ 0 2 + C 1 ⋅ 0 + C 2 = C 2 F H = 0 ⟹ C 2 = 0

Já aplicando a segunda, obtemos:

d y d x x = 0 = 1 F H 14715 ⋅ 0 + C 1 = C 1 F H = 0 ⟹ C 1 = 0

Por fim, aplicando a terceira condição, temos:

3 = 7357,5 ⋅ 15 2 F H ⟹ F H = 551,8 ⋅ k N

Portanto, a equação da corda é:

y = x 2 75

Passo 3

Para finalizarmos a questão, basta descobrirmos a tração mínima na corda. Esta tração ocorrerá no ponto de menor inclinação. Isto é, o ponto em que d y d x = 0 . Portanto, no meio do cabo.

Além disto, o valor mínimo é igual a F H . Portanto,

T m í n = F H = 5 51 , 8   k N

E assim finalizamos a questão!

Resposta

T m í n = 551,8   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cabo suporta três cargas mostradas. Determine a intensidade de P 1 se P 2 = 1500N e y B = 2,4m . Determine também a flecha y D .
O cabo suporta três cargas mostradas. Determine as flechas y B e y D dos pontos B e D . Considere P 1 = 2000N , P 2 = 1250N .
Se os cilindros C e D pesam cada um 5k N , determine a flecha máxima h e o comprimento do cabo entre as polias lisas em A e B . A viga tem um peso por unidade de comprimento de 2k N / m .
Mostre que a curva de deflexão do cabo discutido no Exemplo 7.13 se reduz à equação 4 no exemplo 7.12 quando a função de cosseno hiperbólico é expandida em termos de uma série e apenas os dois primeir
Se a força de reboque horizontal for T = 20k N e a corrente tem uma massa por unidade de comprimento de 15k g / m , determine a flecha máxima h . Despreze o efeito da flutuação da água sobre a corrent